Model Code
This section is a technical documentation of the microWELT 2.0 LTC model, including the model code. It is organised module by module. Each module documentation contains a text description followed by the code. The modules are grouped as follows:
Model Overview
The actors
The socio-demographic core
Long Term Care (LTC)
The simulation engine and associated modules
Table output
This documentation is automatically generated from the latest version of the model code.
Last update: 2025-02-08
Model Overview
MicroWELT 2.0 LTC - is a model built on the MicroWELT microsimulation platform and focuses on projecting long-term care (LTC) demand in hours, care arrangements and care gaps. The model introduces a new and refined x-compatible re-implementation of MicroWELT’s core socio-demographic modules. X-compatibility refers to the ability to compile the source code in two programming technologies, namely Modgen and the new open source environment openM++. Most of the modules have been reimplemented from scratch, adding details where necessary in the context of LTC and removing some “bells and whistles” that, based on user experience, were rarely used. In addition, all socio-economic modules such as labour force processes, retirement and economic accounting were removed as they were not required for this model variant.
In terms of content, the main innovation is the implementation of a new LTC module based on a comparative approach developed in the wellCARE project and documented in the technical paper Comparative Modelling of Long-Term Care in Hours. This novel approach generalises an Austrian administrative procedure for assessing care needs and uses data from the Survey of Health, Ageing and Retirement in Europe (SHARE) to quantify the demand for and supply of long-term care in hours, distinguishing between care in institutions, formal home care, informal spousal care, other informal care and care gaps.
The modelling of long-term care takes into account a wide range of individual and family characteristics available from the core socio-demographic modules of microWELT. Education, the presence of a spouse capable of providing care and the number of children are central. Refinements to the existing socio-demographic core modules include additional detail in the modelling of fertility by parity and more detailed modelling of mortality differentials by education.
The model inherits most of the features of the existing microWELT applications, where microWELT is conceived as a modular, open-source modelling platform that has been developed for the comparative study of the interactions between population ageing, socio-demographic change and welfare state regimes. MicroWELT follows a continuous-time, interacting population framework and supports the alignment of aggregate results with official population projections.
MicroWELT simulates three types of actors (agents), namely observations, persons and an observer. Observations correspond to the records of a starting population file and are created to generate the simulated population by sampling and cloning. Observations are linked to nuclear families. Observations are temporary actors; once the simulated population is created, the observation actors are destroyed. Persons are the main units of the simulation. The single observer actor is used for processes that require aggregated information, such as model alignment. It is also used to improve efficiency, such as having only one calendar year clock rather than individual year change events.
In a nutshell, the model consists of the following components and modeled behaviors, most of which corresponding to various modules which include their own detailed documentation:
The simulation engine, which generates all actors known at the start of the simulation. Most importantly, it generates the initial population from a starting population microdata file.
Education, which takes into account the intergenerational transmission of education and supports trend scenarios as well as scenarios in which changes are driven by the intergenerational transmission of education.
Demography: For mortality and fertility, microWELT reproduces Eurostat’s population projections at the aggregate level, but adds detail at the individual level by taking into account variations in first birth cohort rates and resulting childlessness, progression to second births and longevity by education. Net migration is modelled on the basis of Eurostat projections by age and sex, but with the aim of keeping families together.
Partnerships are modelled from the female perspective, taking into account age, presence and age of children in the family and education. Partners are matched by assortative mating, based on distributions of age differences and education.
LTC needs, arrangements and gaps are modelled, taking into account age, gender and education, as well as the availability of a spouse and the number of children.
Model output is produced through a comprehensive set of output tables.
Model Actors
ActorObservation.mpp
The Observation actor module contains the basic information that defines the Observation actor. Observatios are created as internal representations of the records in the starting population file. They are used to create Person actors of the initial simulated population, which may be smaller or larger than the initial population file. The weights of the observations are used to determine whether and how often an individual observation is represented in the simulated population. All simulated individuals have the same weight. Observation actors are temporary; once the simulated population is created, the Observation actors are destroyed to free up memory space.
In the pre-simulation phase, the file size of the starting population is determined and, based on the record weights and the size of the simulated population, the scaling factor for automatic population scaling of the simulation outputs is determined. The starting population file is a csv-file with a header row containing variable names. Both the file name and the size of the simulation are model parameters. The record layout of the starting population file is defined in this module (PERSON_MICRODATA_COLUMNS).
Variables of the starting population:
Household ID: 1234
Weight: 543.21
Time of birth: 1966 (a random number is added if the time of birth is integer)
Sex: 0 female, 1 male
Education level: 0 (ISCED 2 or lower), 1 (ISCED 3), 2 (ISCED 4), 3 (ISCED 5 or higher)
Role in family: 0 head, 1 spouse, 2 child. (The choice of head is arbitrary; in the simulation, the female partner is considered to be the head)
Currently attending school: 0 no, 1 yes
When the model is extended, new variables need to be added to this list. A link to the corresponding Observation is passed as a parameter to the Start function of the Person actors, so that the values of the variables can be accessed to initialise the Person actors.
Parameters:
File name** of the starting population csv file
Simulation size:** Number of simulated actors representing the initial population. In addition to the simulation size, users can also set the number of replicates (how often the simulation is repeated; run in parallel). This is done in the general scenario settings. A typical simulation size that eliminates most of the Monte Carlo variation in the aggregate results while keeping run times low (depending on computer power, ~1h) is 8 x 400,000.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor-Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN All observations
actor_set Observation asObservations;
//EN Observations by family ID
actor_set Observation asObservationByFam[fam_id];
//EN All oldest observations in family
actor_set Observation asObservationOldest filter obs_oldest;
//EN Simulated oldest observations in family
actor_set Observation asSimulatedObservationOldest filter obs_oldest && obs_weight > 0;
//EN Observations by family ID - oldest
actor_set Observation asObservationByFamOldest[fam_id] filter obs_oldest;
//EN Observations by family ID - excluding oldest
actor_set Observation asObservationByFamNotOldest[fam_id] filter !obs_oldest;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification PERSON_MICRODATA_COLUMNS //EN List of Starting population variables
{
PMC_FAMID, //EN Household ID
PMC_WEIGHT, //EN Weight
PMC_BIRTH, //EN Time of birth
PMC_SEX, //EN Sex
PMC_EDUC, //EN Education level
PMC_ROLE, //EN Role in family
PMC_INSCHOOL //EN Currently attending school
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameters
{
file MicroDataInputFile; //EN File name of starting population
double StartPopSampleSize; //EN Simulated sample size of starting population
model_generated long MicroDataInputFileSize; //EN File size of starting population
model_generated double ScalingFactor; //EN Scaling factor (actor weight)
};
parameter_group P0_ModelSettings //EN Starting population
{
MicroDataInputFile, StartPopSampleSize
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor states and functions
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Observation //EN Actor Observations
{
double pmc[PERSON_MICRODATA_COLUMNS]; //EN Person micro record columns
integer obs_weight = { 1 }; //EN Observation integer weight
FAM_ID fam_id = { 0 }; //EN Family ID
TIME obs_birth = { TIME_INFINITE }; //EN Time of birth
logical obs_oldest = { FALSE }; //EN Is oldest of family
void Start(const input_csv& input); //EN Function starting the actor
void Finish(); //EN Function destroying the actor
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Observation::Start(const input_csv& in_csv)
{
// Initialize all attributes (OpenM++).
initialize_attributes();
for (int nJ = 0; nJ < SIZE(PERSON_MICRODATA_COLUMNS); nJ++)
{
pmc[nJ] = in_csv[nJ];
}
fam_id = (int)pmc[PMC_FAMID];
obs_birth = pmc[PMC_BIRTH];
time = MIN(ALL_YEAR);
// Have the entity enter the simulation (OpenM++).
enter_simulation();
};
void Observation::Finish()
{
// Have the entity exit the simulation (OpenM++).
exit_simulation();
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Pre-Simulation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void PreSimulation()
{
// Open starting population file
input_csv inCsv;
inCsv.open(MicroDataInputFile);
// Determine the starting population file size and scaling factor
long lRecordCount = 0;
double dPopSize = 0.0;
while (inCsv.read_record(lRecordCount))
{
lRecordCount++;
dPopSize = dPopSize + inCsv[PMC_WEIGHT];
}
ScalingFactor = dPopSize / StartPopSampleSize;
MicroDataInputFileSize = lRecordCount - 1;
// Close starting population file
inCsv.close();
}
ActorPerson.mpp
The Person actor module contains the basic information that defines the Person actor. The most important function is the Start() function, which initialises all states of a person at creation. This includes initialising time. When the Start function is called (which is done by the simulation engine to create the initial population and immigrants; and by mothers giving birth) the following parameters are passed to the person:
Creation type: identifies whether a person comes from the starting population file, is an immigrant or enters by birth.
Pointer to observation: for persons created from Observations (the starting population file), this pointer allows access to the variable values from the file.
Pointer to creator: For persons created from the starting population file, this is the oldest person of the family who is created first; for births during the simulation the pointer links to the mother. It allows to access information from the the person and to establish family relationships.
Year of immigration: this parameter is only relevant for immigrants.
Sex of immigrant: this parameter is only relevant for immigrants.
After the Start function, a person is part of the simulation. At this point, immediately after birth, the “SetAliveEvent” event is called, which handles family and other actor links, and calls initialisation functions that require the person to be already in the simulation (and therefore cannot be performed in the Start function).
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor-Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN All Person actors
actor_set Person asAllPerson filter is_alive;
//EN Residets by age and sex
actor_set Person asResidentsAgeSex[integer_age][sex] filter is_alive && is_resident;
//EN Residets by age sex and education
actor_set Person asResidentsAgeSexEduc[integer_age][sex][educ_level3] filter is_alive && is_resident;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification SEX //EN Sex
{
FEMALE, //EN Female
MALE //EN Male
};
classification CREATION_TYPE //EN Creation type
{
CT_START, //EN Person from startpop
CT_CHILD, //EN Person born in simulation
CT_IMMIGRANT //EN Immigrant
};
range AGE_MAX26 { 0, 26 }; //EN Age
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
// Simple states
SEX sex = { FEMALE }; //EN Sex
FAMILY_ROLE family_role_start = { FR_HEAD }; //EN Family role
logical is_resident = { TRUE }; //EN Ever resident
double time_of_birth = { 2000.0 }; //EN Time of birth
ALL_YEAR year_of_birth = { 2000 }; //EN Year of birth
CREATION_TYPE creation_type = { CT_START }; //EN Creation type
Person_ptr ptr_creator; //EN Pointer to creator
// Derived states
AGE_MAX26 age_max26 = COERCE(AGE_MAX26, integer_age); //EN Age
SIM_YEAR sim_year = COERCE(SIM_YEAR, calendar_year); //EN Year
logical in_projected_time = (calendar_year >= MIN(SIM_YEAR)); //EN In projected time
AGE_65P age_65p = COERCE(AGE_65P, integer_age); //EN Age
// Functions
//EN Start
void Start(CREATION_TYPE cCreationType, // Creation type
Observation_ptr prObs, // Pointer to observation
Person_ptr prCreator, // Pointer to creator
int nYearOfImmigration, // Year of immigration
SEX nImmiSex); // Sex of immigrant
void Finish(); //EN Finish
event timeSetAliveEvent, SetAliveEvent; //EN Set alive
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Person::Start(CREATION_TYPE cCreationType, Observation_ptr prObs, Person_ptr prCreator, int nYearOfImmigration, SEX cImmiSex)
{
// Initialize all attributes (OpenM++)
initialize_attributes();
// Setting the actor weight (Modgen only)
Set_actor_weight(ScalingFactor); Set_actor_subsample_weight(ScalingFactor);
TIME dTime = 0.0;
creation_type = cCreationType;
if (prCreator) ptr_creator = prCreator;
else ptr_creator = NULL;
// Person from starting population
if (creation_type == CT_START)
{
// Determine time (cannot be born before creator)
dTime = prObs->pmc[PMC_BIRTH];
if (int(dTime) == dTime) dTime = dTime + RandUniform(2);
if (ptr_creator && dTime < ptr_creator->time_of_birth) dTime = ptr_creator->time_of_birth + 0.00001;
// Initialise states
is_resident = TRUE;
sex = (SEX)(int)prObs->pmc[PMC_SEX];
family_role_start = (FAMILY_ROLE)(int)prObs->pmc[PMC_ROLE];
educ_start = (EDUC_LEVEL4)(int)prObs->pmc[PMC_EDUC];
in_educ_start = ((int)prObs->pmc[PMC_INSCHOOL] == 1) ? TRUE : FALSE;
}
// Person born in simulation
else if (creation_type == CT_CHILD)
{
dTime = ptr_creator->time;
is_resident = TRUE;
double dSexRatio = SexRatio[RANGE_POS(SIM_YEAR, int(dTime))];
if (RandUniform(30) < dSexRatio / (100.0 + dSexRatio)) sex = MALE;
else sex = FEMALE;
}
// Immigrants
else if (creation_type == CT_IMMIGRANT)
{
is_resident = FALSE;
sex = cImmiSex;
time_of_immigration = nYearOfImmigration + RandUniform(42);
is_unattended = TRUE;
int nAgeAtImmigration;
Lookup_AgeImmigrants(RandUniform(43), sex, RANGE_POS(SIM_YEAR, nYearOfImmigration), &nAgeAtImmigration);
dTime = time_of_immigration - nAgeAtImmigration - RandUniform(44);
}
// All
age = 0;
time = dTime;
calendar_year = int(time);
time_of_birth = time;
year_of_birth = int(time);
// Have the entity enter the simulation (OpenM++).
enter_simulation();
}
void Person::Finish()
{
is_alive = FALSE;
// Have the entity exit the simulation (OpenM++).
exit_simulation();
}
TIME Person::timeSetAliveEvent()
{
if (!is_alive) return WAIT(0.0);
else return TIME_INFINITE;
}
void Person::SetAliveEvent()
{
// Set alive and link to Observer
is_alive = TRUE;
lObserver = asObserver->Item(0);
// Link family members in starting population
if ((creation_type == CT_START && ptr_creator) || creation_type == CT_CHILD) LinkToFamilyWhenSetAlive();
// Assign education
if (creation_type == CT_START || creation_type == CT_CHILD)
{
setParentsEducAtBirth();
setEducAtBirth();
}
else if (creation_type == CT_IMMIGRANT)
{
setImmiEducAtBirth();
}
// Assign lifetime childlessness for men
if (sex == MALE && (creation_type == CT_CHILD || creation_type == CT_IMMIGRANT))
{
setMaleLifetimeChildlessnessAtBirth();
}
// Initiate slower ageing for LTC
InitTimeNextLtcAgeUpdate();
}
ActorObserver.mpp
The Observer module contains the basic information associated with an Observer actor. A single Observer actor is instantiated in a simulation. All people are linked to the Observer at birth. The Observer is mainly used for alignment and to improve efficiency, e.g. by implementing a single year change clock instead of year change events at the individual level. At the beginning and end of each year, and in the middle of each month, clock events are called, which are used to call functions to be performed at those times. For example, at the beginning of each year the observer loops through the whole population and calls an individual level function that handles the year change, e.g. by incrementing the calendar year.
At the end of the year, just before the projected time begins, a series of initialisation functions are called. These include functions for imputing the number of children, including those not currently observed in the family, and the initial initialisation of long-term care needs and arrangements, which are then updated according to a mid-month schedule. These functions - as well as other functionalities of the Observer - are implemented and documented in the relevant modules.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Links & Actor Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
link Person.lObserver Observer.mlObserverToPerson[]; //EN Link between person and observer
actor_set Observer asObserver; //EN Actor set Observer
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Observer //EN Actor for synchronising population-level activities
{
void Start();
void Finish();
int observer_year = { 1900 }; //EN Calendar Year
ALL_YEAR observer_tab_year = COERCE(ALL_YEAR, observer_year); //EN Year
TIME next_observer_year_end = { TIME_INFINITE }; //EN Time of next calendar year end
event timeObserverYearEndEvent, ObserverYearEndEvent; //EN Year end event
TIME next_observer_year_start = { TIME_INFINITE }; //EN Time of next calendar year start
event timeObserverYearStartEvent, ObserverYearStartEvent; //EN Year start event
TIME next_observer_midmonth = { TIME_INFINITE }; //EN Time of next mid-month
event timeObserverMidMonthEvent, ObserverMidMonthEvent; //EN Mid-month event
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Observer::Start()
{
// Initialize all attributes (OpenM++).
initialize_attributes();
time = MIN(ALL_YEAR);
observer_year = int(time);
age = 0;
next_observer_year_end = WAIT(0.0);
next_observer_midmonth = WAIT(1.0 / 24.0);
if (ModelMigration) next_emigration_event = MIN(SIM_YEAR) + 0.5;
doInitParentsEducArray();
// Have the entity enter the simulation (OpenM++).
enter_simulation();
}
void Observer::Finish()
{
// Have the entity exit the simulation (OpenM++).
exit_simulation();
}
// Calendar year change
TIME Observer::timeObserverYearStartEvent() { return next_observer_year_start; }
TIME Observer::timeObserverYearEndEvent() { return next_observer_year_end; }
TIME Observer::timeObserverMidMonthEvent() { return next_observer_midmonth; }
void Observer::ObserverYearEndEvent()
{
int nPerson = asAllPerson->Count();
for (int nJ = 0; nJ < nPerson; nJ++)
{
Person_ptr paPerson = asAllPerson->Item(nJ);
paPerson->YearEnd();
}
// End of last year before simulation starts
if (observer_year == MIN(SIM_YEAR) - 1)
{
ImputeObservedNumberChildren();
ImputeNumberChildren50p();
ImputeFirstAndSecondBirths36to49();
ImputeUnobservedFirstBeforeObservedBirths();
SetRemainingFertilityStatesAtSimulationStart();
ImputeMaleParity();
UpdateLontermCare();
}
next_observer_year_end = WAIT(1.0);
next_observer_year_start = WAIT(0.0);
}
void Observer::ObserverYearStartEvent()
{
observer_year = int(time);
resetEducStack();
int nPerson = asAllPerson->Count();
for (int nJ = 0; nJ < nPerson; nJ++)
{
Person_ptr paPerson = asAllPerson->Item(nJ);
paPerson->YearStart();
}
next_observer_year_start = TIME_INFINITE;
}
void Observer::ObserverMidMonthEvent()
{
if (observer_year >= MIN(SIM_YEAR))
{
UpdatePartnershipStatus();
UpdateLontermCare();
}
next_observer_midmonth = WAIT(1.0/12.0);
}
The Socio-Demographic Core
Fertility.mpp
The fertility module implements births, including the imputation of past births. It is designed to simultaneously match official population projections - i.e. aggregate age-specific birth rates - and to take into account education-specific differences in age at first birth and the distribution of family sizes (0, 1, 2+ children). Family sizes are parameterised by education-specific cohort parameters, namely first birth rates by age and second birth rates by time since first birth. Children observed in the starting population are considered as own children.
First and second births that cannot be observed in the starting population because the children have already moved out are imputed, the algorithm depending on the age group:
For women aged 50+, the number of children is imputed by age and education (from a parameter). In addition, log odds are used to select women (of a given education and age) by their current partnership status. The algorithm takes into account observed children in the family, so the number of children can only increase.
Women under 36 are assumed to live with all their children, so family size is assumed to be equal to the observed number of children in the family.
Women aged 36-49: Based on first birth rates, the number of women expected to be a mother is calculated for each education group and age. This number is compared with the number of observed mothers and the gap is closed by finding suitable women who are assumed to have given birth more than 18 years ago (i.e. to children who have already moved out and therefore cannot be observed in the starting population). Once these women have been identified (as in the case of first births, the algorithm also takes into account current partnership status), the date of first birth is assigned. For the remaining time window (from the imputed first birth to 18 years before the start of the simulation), second births are assigned according to second birth rates. While this algorithm is intended to be a realistic allocation of motherhood, the number of second births so far does not take into account cases where one child is observed in the family but this child is not the first child, i.e. the first child has already moved out. To account for these cases, the probability that an observed single child actually has an older sibling is calculated and additional first births are imputed.
The fertility module focuses on women. Apart from the observed number of children from the starting population, family characteristics from the male perspective are treated in a separate module.
Within the simulation, births are modeled the following way:
Birth events are created based on age-specific period rates. The women triggering the event are not considered to be the mothers; the most likely women of similar age to give birth still has to be identified.
Events for expected first births are created by applying education and cohort-specific first birth rates. Women expecting a first birth are given first priority to become the mothers of the babies created by the birth events. Applying age-sepcific first birth rates implicitly determines education-specific cohort childlessness.
Events for expecting a second birth are created by applying education and cohort specific second birth rates. Women expecting a second birth are prioritised to become the mothers of the babies created by the birth events if no woman expects a first birth.
Higher order births are randomly assigned to women of the given age who already have two or more children.
Parameters:
Age-specific fertility rates: this parameter is usually taken from official population projections. As explained above, it is used as an adjustment target, creating birth events without deciding which woman of the given age will be the mother of the child.
First birth cohort rates by education: This (age-specific) parameter - available e.g. from the Human Fertility Database - is used to model ‘expected’ first births. The parameter is also used to impute past births that cannot be observed in the starting population because the children have already moved out. As the required cohort data are only available for the past and are age-censored for cohorts that have not yet reached the end of their reproductive life, the parameterisation requires scenario assumptions.
Duration-specific parity progression to second child by education: This parameter is used to model ‘expected’ second births by time since first birth. The parameter is also used to impute past births that cannot be observed in the starting population because the children have already moved out. Obtaining this parameter typically involves estimation from survey data and calibration to scenario-based projections of education-specific parity progressions.
Distribution of number of children by age and education for women aged 50+. This parameter is used to impute family size. It is usually obtained from retrospective information collected in survey data such as SHARE.
Odds ratio of having at least one child comparing women in a couple with single women by age group. This parameter is used to impute family size to women aged 50 and over. It is usually estimated from retrospective information collected in survey data such as SHARE.
Odds ratios of having two or more children comparing mothers in a partnership with mothers not currently in a partnership, by age group. This parameter is used to impute family size to women aged 50 and over. It is usually estimated from retrospective information collected in survey data such as SHARE.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN Women by education and family size
actor_set Person asWomenByEducFamilySize[year_of_birth][educ_level3][has_spouse][number_children2]
filter sex == FEMALE && is_alive && is_resident;
//EN Fertile women by fertility status
actor_set Person asFertileWomenByStatus[fertile_age][fertility_status]
filter in_projected_time && sex == FEMALE && WITHIN(FERTILE_AGE,integer_age)
&& (waiting_for_first_birth || waiting_for_second_birth || ready_for_higher_birth)
&& is_alive && is_resident;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification NUMBER_CHILDREN2 //EN Number Children
{
NC2_0, //EN No children
NC2_1, //EN One child
NC2_2P //EN Two or more children
};
classification FERTILITY_STATUS //EN Fertility status
{
FST_WAIT_FIRST, //EN Waiting for first birth
FST_WAIT_SECOND, //EN Waiting for second birth
FST_READY_3P //EN Ready for 3rd and higher order birth
};
classification CHILD_ORDER2 //EN Child order
{
CO2_1, //EN First child
CO2_2P //EN Second child
};
range FERTILE_AGE { 15, 49 }; //EN Age
range FERT_PROG { 0, 12 }; //EN Years since first birth
partition ORCHILD_AGEGROUP { 65, 75, 85 }; //EN Age group
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG_CHILDREN //EN Fertility
{
NumberChildren50p,
OddsRatioAnyChildrenIfCouple,
OddsRatio2PChildrenIfCouple,
FirstBirthCohortRates,
ParityProgressionSecond,
AgeSpecificFertility,
SexRatio
};
parameters
{
double NumberChildren50p[EDUC_LEVEL3][YOB_START_50P][NUMBER_CHILDREN2]; //EN Distribution number of children 50+
double OddsRatioAnyChildrenIfCouple[ORCHILD_AGEGROUP]; //EN Odds Ratio any children if in partnership
double OddsRatio2PChildrenIfCouple[ORCHILD_AGEGROUP]; //EN Odds Ratio 2+ children if in partnership
double FirstBirthCohortRates[EDUC_LEVEL3][FERTILE_AGE][YOB_BIRTH1]; //EN First birth cohort rates
double ParityProgressionSecond[EDUC_LEVEL3][YOB_BIRTH1][FERT_PROG]; //EN Parity progression 2nd child
double AgeSpecificFertility[FERTILE_AGE][SIM_YEAR]; //EN Age specific fertility rate
double SexRatio[SIM_YEAR]; //EN Sex Ratio (males per 100 females)
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Observer
{
void ImputeObservedNumberChildren(); //EN Impute observed number of children
void ImputeNumberChildren50p(); //EN Impute number of children 50+
void ImputeFirstAndSecondBirths36to49(); //EN Impute first births women 36-49 at start
void ImputeUnobservedFirstBeforeObservedBirths(); //EN Impute unobseerved first births before observed
void SetRemainingFertilityStatesAtSimulationStart(); //EN Set remaining fertility-related states at start
};
actor Person
{
int sim_births = { 0 }; //EN Births in simulation
int sim_higher_births = { 0 }; //EN Third and higher order births
NUMBER_CHILDREN2 number_children2 = { NC2_0 }; //EN Number children
double time_first_birth = { TIME_INFINITE }; //EN Time of first birth
double time_second_birth = { TIME_INFINITE }; //EN Time of second birth
logical first_birth_is_imputed = { FALSE }; //EN First birth is imputed
logical waiting_for_first_birth = { FALSE }; //EN Waiting for first birth
logical waiting_for_second_birth = { FALSE }; //EN Waiting for second birth
logical ready_for_higher_birth = { FALSE }; //EN Ready for 3rd and higher order birth
FERTILE_AGE fertile_age = COERCE(FERTILE_AGE, integer_age); //EN Age
//EN Fertility status
FERTILITY_STATUS fertility_status =
(waiting_for_first_birth) ? FST_WAIT_FIRST :
(waiting_for_second_birth) ? FST_WAIT_SECOND : FST_READY_3P;
//EN Years since first birth
int years_since_first_birth = { 99 }; //EN Years since first birth
TIME time_next_year_since_first_birth = { TIME_INFINITE }; //EN Next year index change for years since first birth
event timeYearsSinceFirstBirthEvent, YearsSinceFirstBirthEvent; //EN Year index change event for years since first birth
void GetBaby(); //EN Get a baby
event timeFirstBirthFlagEvent, FirstBirthFlagEvent; //EN First birth event
event timeSecondBirthFlagEvent, SecondBirthFlagEvent; //EN Second birth event
event timeBirthEvent, BirthEvent; //EN Birth event
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
TIME Person::timeYearsSinceFirstBirthEvent()
{
if (number_children2 == NC2_1) return time_next_year_since_first_birth;
else return TIME_INFINITE;
}
void Person::YearsSinceFirstBirthEvent()
{
if (years_since_first_birth < MAX(FERT_PROG))
{
years_since_first_birth++;
time_next_year_since_first_birth = WAIT(1.0);
}
else
{
years_since_first_birth = 99;
time_next_year_since_first_birth = TIME_INFINITE;
}
}
//////////////////////////////////
// Imputations
//////////////////////////////////
void Observer::ImputeObservedNumberChildren()
{
int nPopSize = asAllPerson->Count();
for (int nI = 0; nI < nPopSize; nI++)
{
auto prPerson = asAllPerson->Item(nI);
if (prPerson->children_in_family == 1)
{
prPerson->number_children2 = NC2_1;
}
else if (prPerson->children_in_family > 1)
{
prPerson->number_children2 = NC2_2P;
}
else prPerson->number_children2 = NC2_0;
if (prPerson->number_children2 != NC2_0)
{
prPerson->time_first_birth = prPerson->tob_oldest_child_in_family;
}
}
}
void Observer::ImputeNumberChildren50p()
{
for (int nEduc = 0; nEduc < SIZE(EDUC_LEVEL3); nEduc++)
{
for (int nYob = MIN(YOB_START_50P); nYob <= MAX(YOB_START_50P); nYob++)
{
int nAgeIndex = SPLIT(MIN(SIM_YEAR) - nYob, ORCHILD_AGEGROUP);
// Childless versus mothers
int nChildlessSingle = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count();
int nChildlessCouple = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count();
int nMotherSingle = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_2P]->Count();
int nMotherCouple = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_2P]->Count();
double dExpectedMothers = double(nChildlessSingle + nChildlessCouple + nMotherSingle + nMotherCouple) *
((NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_1]
+ NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_2P]) /
(NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_0]
+ NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_1]
+ NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_2P]));
while (nMotherSingle + nMotherCouple < dExpectedMothers
&& (asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count() > 0))
{
double dWeightedCouple = OddsRatioAnyChildrenIfCouple[nAgeIndex] * double(asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count());
double dWeightedAll = dWeightedCouple
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count();
// apply odds ratio to decide picking a single woman or woman with partner
logical bSelectCouple = FALSE;
if (RandUniform(9) < dWeightedCouple / dWeightedAll) bSelectCouple = TRUE;
if ((bSelectCouple && asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count() > 0)
|| asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count() == 0)
{
auto prPerson = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->GetRandom(RandUniform(10));
prPerson->number_children2 = NC2_1;
nMotherCouple++;
}
else
{
auto prPerson = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->GetRandom(RandUniform(11));
prPerson->number_children2 = NC2_1;
nMotherSingle++;
}
}
// One versus 2+ children
int nOneChildSingle = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->Count();
int nMoreChildrenSingle = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_2P]->Count();
int nOneChildCouple = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->Count();
int nMoreChildrenCouple = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_2P]->Count();
double dExpected2p = double(nOneChildSingle + nMoreChildrenSingle + nOneChildCouple + nMoreChildrenCouple) *
(NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_2P] /
(NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_1]
+ NumberChildren50p[nEduc][RANGE_POS(YOB_START_50P, nYob)][NC2_2P]));
while (nMoreChildrenSingle + nMoreChildrenCouple < dExpected2p
&& (asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->Count() > 0))
{
double dWeightedCouple = OddsRatio2PChildrenIfCouple[nAgeIndex] * double(asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->Count());
double dWeightedAll = dWeightedCouple
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->Count();
// apply odds ratio to decide picking a single woman or woman with partner
logical bSelectCouple = FALSE;
if (RandUniform(12) < dWeightedCouple / dWeightedAll) bSelectCouple = TRUE;
if ((bSelectCouple && asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->Count() > 0)
|| asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->Count() == 0)
{
auto prPerson = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->GetRandom(RandUniform(13));
prPerson->number_children2 = NC2_2P;
nMoreChildrenCouple++;
}
else
{
auto prPerson = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->GetRandom(RandUniform(15));
prPerson->number_children2 = NC2_2P;
nMoreChildrenSingle++;
}
}
}
}
}
void Observer::ImputeFirstAndSecondBirths36to49()
{
int nMothers = 0;
int nExpectedMothers = 0;
int nWomen = 0;
for (int nEduc = 0; nEduc < SIZE(EDUC_LEVEL3); nEduc++)
{
for (int nYob = MIN(YOB_START_36TO49); nYob <= MAX(YOB_START_36TO49); nYob++)
{
int nAgeIndex = SPLIT(MIN(SIM_YEAR) - nYob, ORCHILD_AGEGROUP);
// Calculate number of expected mothers
nMothers = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_1]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_1]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_2P]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_2P]->Count();
nWomen = nMothers
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count();
double dChildless = 1.0;
for (int nAgeIndex = 0; nAgeIndex < SIZE(FERTILE_AGE) && nYob + MIN(FERTILE_AGE) + nAgeIndex < MIN(SIM_YEAR); nAgeIndex++)
{
dChildless = dChildless * exp(-FirstBirthCohortRates[nEduc][nAgeIndex][RANGE_POS(YOB_BIRTH1, nYob)]);
}
nExpectedMothers = round(nWomen * (1 - dChildless));
// Impute motherhood & date of first birth
while (nMothers < nExpectedMothers
&& (asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count()
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count() > 0))
{
double dWeightedCouple = OddsRatioAnyChildrenIfCouple[nAgeIndex] * double(asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count());
double dWeightedAll = dWeightedCouple
+ asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count();
Person_ptr prPerson = NULL;
// Motherhood
logical bSelectCouple = FALSE;
if (RandUniform(16) < dWeightedCouple / dWeightedAll) bSelectCouple = TRUE;
if ((bSelectCouple && asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->Count() > 0)
|| asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->Count() == 0)
{
prPerson = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][TRUE][NC2_0]->GetRandom(RandUniform(17));
}
else
{
prPerson = asWomenByEducFamilySize[RANGE_POS(ALL_YEAR, nYob)][nEduc][FALSE][NC2_0]->GetRandom(RandUniform(18));
}
prPerson->number_children2 = NC2_1;
nMothers++;
// Date of first birth
double dProbBirth[SIZE(FERTILE_AGE)];
double dSurvivalChildless = 1.0;
double dSum = 0.0;
double dSumProb = 0.0;
bool bFound = FALSE;
double dRandom = RandUniform(19);
for (int nAgeIndex = 0; nAgeIndex < MIN(SIM_YEAR) - nYob - 19 - MIN(FERTILE_AGE); nAgeIndex++)
{
dProbBirth[nAgeIndex] = dSurvivalChildless * (1.0 - exp(-FirstBirthCohortRates[nEduc][nAgeIndex][RANGE_POS(YOB_BIRTH1, nYob)]));
dSurvivalChildless = dSurvivalChildless * exp(-FirstBirthCohortRates[nEduc][nAgeIndex][RANGE_POS(YOB_BIRTH1, nYob)]);
dSum = dSum + dProbBirth[nAgeIndex];
}
for (int nAgeIndex = 0; nAgeIndex < MIN(SIM_YEAR) - nYob - 19 - MIN(FERTILE_AGE) && !bFound; nAgeIndex++)
{
dSumProb = dSumProb + dProbBirth[nAgeIndex] / dSum;
if (dRandom < dSumProb)
{
bFound = TRUE;
prPerson->time_first_birth = prPerson->time_of_birth + MIN(FERTILE_AGE) + nAgeIndex + RandUniform(20);
prPerson->first_birth_is_imputed = TRUE;
// 2nd birth
bool bSecond = FALSE;
double dTimeAtRiskSecondBirth = MIN(SIM_YEAR) - 18 - prPerson->time_first_birth;
int nPeriod = 0;
while (nPeriod < SIZE(FERT_PROG) && nPeriod < dTimeAtRiskSecondBirth && !bSecond && nAgeIndex + nPeriod < MIN(SIM_YEAR) - nYob - 19 - MIN(FERTILE_AGE))
{
double dHazard = ParityProgressionSecond[nEduc][RANGE_POS(YOB_BIRTH1, nYob)][nPeriod];
double dWait = TIME_INFINITE;
if (dHazard > 0) dWait = -log(RandUniform(21)) / dHazard;
if (dWait < 1.0)
{
bSecond = TRUE;
prPerson->time_second_birth = prPerson->time_first_birth + nPeriod + dWait;
prPerson->number_children2 = NC2_2P;
}
else nPeriod++;
}
}
}
}
}
}
}
void Observer::ImputeUnobservedFirstBeforeObservedBirths()
{
int nPersons = asAllPerson->Count();
for (int nIndex = 0; nIndex < nPersons; nIndex++)
{
Person_ptr prPerson = asAllPerson->Item(nIndex);
if (prPerson->sex == FEMALE && prPerson->is_resident && !prPerson->first_birth_is_imputed && prPerson->number_children2 == NC2_1 &&
prPerson->integer_age >= 36 && prPerson->integer_age <= 49)
{
int nAgeAtObservedBirth = (int)(prPerson->tob_oldest_child_in_family - prPerson->time_of_birth);
int nYob = prPerson->year_of_birth;
// Probability of observation without previous birth
double dProbFirst = 1.0;
for (int nAge = MIN(FERTILE_AGE); nAge <= nAgeAtObservedBirth; nAge++)
{
double dBirthRate = FirstBirthCohortRates[prPerson->educ_level3][RANGE_POS(FERTILE_AGE, nAge)][RANGE_POS(YOB_BIRTH1, nYob)];
double dBirthProb = 1.0 - exp(-dBirthRate);
if (nAge < nAgeAtObservedBirth) dProbFirst = dProbFirst * (1.0 - dBirthProb);
else dProbFirst = dProbFirst * dBirthProb;
}
// Probability of observation with previous birth
int nMaxAgeUnobserved = (int)(time - 19.0 - prPerson->time_of_birth);
if (nMaxAgeUnobserved > nAgeAtObservedBirth) nMaxAgeUnobserved = nAgeAtObservedBirth; //observed is > 18
double dProbSecond = 0.0;
double dSumProbSecond = 0.0;
for (int nAgeFirst = MIN(FERTILE_AGE); nAgeFirst <= nMaxAgeUnobserved; nAgeFirst++)
{
dProbSecond = 1.0;
for (int nAge = MIN(FERTILE_AGE); nAge <= nAgeAtObservedBirth; nAge++)
{
if (nAge <= nAgeFirst)
{
double dBirthRate = FirstBirthCohortRates[prPerson->educ_level3][RANGE_POS(FERTILE_AGE, nAge)][RANGE_POS(YOB_BIRTH1, nYob)];
double dBirthProb = 1.0 - exp(-dBirthRate);
if (nAge < nAgeFirst) dProbSecond = dProbSecond * (1.0 - dBirthProb);
else dProbSecond = dProbSecond * dBirthProb;
}
else
{
int nFertProg = nAge - nAgeFirst - 1;
if (!WITHIN(FERT_PROG, nFertProg)) dProbSecond = 0; // Period between births too long
else
{
double dBirthRate = ParityProgressionSecond[prPerson->educ_level3][RANGE_POS(YOB_BIRTH1, nYob)][nFertProg];
double dBirthProb = 1.0 - exp(-dBirthRate);
if (nAge < nAgeAtObservedBirth) dProbSecond = dProbSecond * (1.0 - dBirthProb);
else dProbSecond = dProbSecond * dBirthProb;
}
}
}
dSumProbSecond = dSumProbSecond + dProbSecond;
}
// Sample if first birth is added
if (RandUniform(22) < dSumProbSecond / (dSumProbSecond + dProbFirst))
{
prPerson->number_children2 = NC2_2P;
}
}
}
}
void Observer::SetRemainingFertilityStatesAtSimulationStart()
{
int nPersons = asAllPerson->Count();
for (int nIndex = 0; nIndex < nPersons; nIndex++)
{
Person_ptr prPerson = asAllPerson->Item(nIndex);
if (prPerson->sex == FEMALE && prPerson->is_resident && prPerson->number_children2 == NC2_1 && prPerson->time_first_birth < time)
{
double dTimeSinceFirstBirth = time - prPerson->time_first_birth;
int nTimeSinceFirstBirth = int(dTimeSinceFirstBirth);
if (nTimeSinceFirstBirth <= MAX(FERT_PROG))
{
prPerson->years_since_first_birth = nTimeSinceFirstBirth;
prPerson->time_next_year_since_first_birth = WAIT(dTimeSinceFirstBirth - nTimeSinceFirstBirth);
}
else
{
prPerson->years_since_first_birth = 99;
prPerson->time_next_year_since_first_birth = TIME_INFINITE;
}
}
if (prPerson->sex == FEMALE && prPerson->is_resident && prPerson->number_children2 == NC2_2P)
{
prPerson->ready_for_higher_birth = TRUE;
}
}
}
//////////////////////////////////
// Births in simulation
//////////////////////////////////
void Person::GetBaby()
{
// Find a spouse if not in a partnership
if (!has_spouse) FindSpouse();
// Create the baby
Person_ptr ptrPerson = new Person();
ptrPerson->Start(CT_CHILD, NULL, this, 0, MALE);
sim_births++;
if (number_children2 == NC2_0)
{
number_children2 = NC2_1;
waiting_for_first_birth = FALSE;
time_next_year_since_first_birth = WAIT(1.0);
years_since_first_birth = 0;
}
else if (number_children2 == NC2_1)
{
number_children2 = NC2_2P;
waiting_for_second_birth = FALSE;
ready_for_higher_birth = TRUE;
}
else
{
sim_higher_births++;
}
}
TIME Person::timeBirthEvent()
{
TIME dEventTime = TIME_INFINITE;
if (in_projected_time && is_resident && sex == FEMALE && WITHIN(FERTILE_AGE, integer_age))
{
double dHazard = AgeSpecificFertility[RANGE_POS(FERTILE_AGE, fertile_age)][RANGE_POS(SIM_YEAR, calendar_year)];
if (dHazard > 0.0) dEventTime = WAIT(-log(RandUniform(26)) / dHazard);
}
return dEventTime;
}
void Person::BirthEvent()
{
Person_ptr prMother = NULL;
// Anybody waiting for first birth?
if (asFertileWomenByStatus[RANGE_POS(FERTILE_AGE, fertile_age)][FST_WAIT_FIRST]->Count() > 0)
{
prMother = asFertileWomenByStatus[RANGE_POS(FERTILE_AGE, fertile_age)][FST_WAIT_FIRST]->GetRandom(RandUniform(27));
}
// Second birth?
else if (asFertileWomenByStatus[RANGE_POS(FERTILE_AGE, fertile_age)][FST_WAIT_SECOND]->Count() > 0)
{
prMother = asFertileWomenByStatus[RANGE_POS(FERTILE_AGE, fertile_age)][FST_WAIT_SECOND]->GetRandom(RandUniform(28));
}
// Higher order
else if (asFertileWomenByStatus[RANGE_POS(FERTILE_AGE, fertile_age)][FST_READY_3P]->Count() > 0)
{
prMother = asFertileWomenByStatus[RANGE_POS(FERTILE_AGE, fertile_age)][FST_READY_3P]->GetRandom(RandUniform(29));
}
// If mother is found, she gets a baby
if (prMother) prMother->GetBaby();
}
TIME Person::timeFirstBirthFlagEvent()
{
TIME dEventTime = TIME_INFINITE;
if (in_projected_time && is_resident && sex == FEMALE && WITHIN(FERTILE_AGE, integer_age)
&& number_children2 == NC2_0 && !waiting_for_first_birth)
{
double dHazard = FirstBirthCohortRates[educ_level3][RANGE_POS(FERTILE_AGE, fertile_age)][RANGE_POS(YOB_BIRTH1, year_of_birth)];
if (dHazard > 0.0) dEventTime = WAIT(-log(RandUniform(23)) / dHazard);
}
return dEventTime;
}
void Person::FirstBirthFlagEvent()
{
waiting_for_first_birth = TRUE;
}
TIME Person::timeSecondBirthFlagEvent()
{
TIME dEventTime = TIME_INFINITE;
if (in_projected_time && is_resident && sex == FEMALE && WITHIN(FERTILE_AGE, integer_age)
&& number_children2 == NC2_1 && !waiting_for_second_birth)
{
if (WITHIN(FERT_PROG, years_since_first_birth))
{
double dHazard = ParityProgressionSecond[educ_level3][RANGE_POS(YOB_BIRTH1, year_of_birth)][years_since_first_birth];
if (dHazard > 0.0) dEventTime = WAIT(-log(RandUniform(25)) / dHazard);
}
}
return dEventTime;
}
void Person::SecondBirthFlagEvent()
{
waiting_for_second_birth = TRUE;
}
Mortality.mpp
The mortality module implements mortality by age, sex and education. It is designed for cases where mortality projections taking into account educational differences are not readily available, but have to be derived by combining information from (1) official population projections with (2) data and scenarios on remaining life expectancy at ages 25 and 65 by education and (3) age-specific mortality differences (relative risks) by education observed today. In terms of educational attainment, this module distinguishes between three levels: low (ISCED 2 and below), medium (ISCED 3 and 4) and high (ISCED 5 and above).
Users have three choices of how to simulate mortality:
Base model: This option does not model mortality by education, but simply applies aggregate period mortality rates by age and sex (typically taken from official population projections).
Detailed model: This option models mortality by education using target remaining life expectancies at ages 25 and 65 and relative risk profiles from parameters. For each year and level of education, the period mortality rates of the base model are calibrated to produce education-specific period life tables. (This step is performed in the pre-simulation function of this module).
Detailed model adjusted to base model total mortality: This option additionally adjusts mortality by age and sex to the base model. This means that mortality projections taken from official population projections are reproduced in aggregate (by age and sex), while maintaining the relative risk structure between education groups.
In order to construct education-specific life tables, two calibration factors by education level (applied together with the age patterns in relative risks) are determined by numerical simulation (binary search). First, a calibration factor is sought to fit the remaining life expectancy at age 65. Second, using this factor for the 65+ population, another calibration factor is determined for the younger ages to fit the remaining life expectancy at age 25. As relative risks by education usually have an age shape (relative differences typically decrease with age), the calibration factors are applied together with the parameter of current age-specific relative risks. In other words, individual mortality is calculated by applying the relative risk factor - rescaled by the calibration factors - to the mortality rate by age and sex taken from official population projections. The underlying assumption is that age patterns in relative risks remain the same over time. For the starting year, this approach is consistent with the direct application of life tables by education (as far as the remaining life expectancies in the parameters are consistent with these life tables), so no calibration is required at the start.
The parameterisation allows the creation of scenarios for the evolution of educational differences in life expectancy, such as convergence scenarios where the gaps between groups narrow or close.
The third model option allows for an additional adjustment of the results of the education-specific model to the aggregate mortality of the base model. This adjustment preserves the relative differences in mortality risks by education. It is implemented by separating the birth events by age and sex produced by the base model from the selection of those selected to die, the latter being based on individual random waiting times taking education into account. Statistically, this approach is equivalent to modifying the baseline mortality hazard (but maintaining the relative risks by education) in such a way that, for a given composition of the population by education, the overall mortality rate is equal to the target mortality rate.
Parameters:
Model option: allows the user to choose between the three model options described above.
Period mortality by age and sex: this parameter is usually taken from official population projections.
Remaining life expectancy at ages 25 and 65 by education, sex and period. Recent estimates are available in the literature and/or can be calculated from period mortality rates by age, sex, and education. The parameter allows the construction of scenarios on the evolution of educational differences, e.g. concergence scenarios.
Current age-specific relative mortality risks by education and sex. This parameter can be calculated by comparing mortality rates by age, sex and education with mortality rates by age and sex. The parameter is used to capture the age patterns in relative risks, but - due the model alignments described above - does not affect education-specific life expectancies.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN All mortal persons
actor_set Person asAllMortalPersonsForMortalityAlignment[sex][integer_age]
filter SelectedMortalityModel == MOM_ALIGNED && in_projected_time && is_alive && is_resident;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification MORTALITY_MODEL //EN Mortality model selection
{
MOM_BASE, //EN Base model
MOM_DETAIL, //EN Detailed model
MOM_ALIGNED //EN Detailed model aligned to base
};
classification LIFE_EXPECT //EN Life Expectancy
{
LE_25, //EN Life expectancy at 25
LE_65 //EN Life expectancy at 65
};
range AGE_RANGE { 0, 105 }; //EN Age
range AGE_25P { 25, 105 }; //EN Age
range AGE_65P { 65, 105 }; //EN Age
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG02_Mortality //EN Mortality
{
SelectedMortalityModel,
MortalityTable,
LifeExpectancy,
MortalityAdjustment
};
parameters
{
MORTALITY_MODEL SelectedMortalityModel; //EN Mortality model selection
double MortalityTable[SEX][AGE_RANGE][SIM_YEAR]; //EN Mortality base rates
double LifeExpectancy[SEX][LIFE_EXPECT][SIM_YEAR][EDUC_LEVEL3]; //EN Period life expectancy
double MortalityAdjustment[SEX][AGE_25P][EDUC_LEVEL3]; //EN Mortality relative risks profile
//EN Mortality hazards by education
model_generated double MortalityDetailedHazard[SEX][EDUC_LEVEL3][AGE_RANGE][SIM_YEAR];
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor states and functions
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
logical is_alive = { FALSE }; //EN Alive
void HandleMortality(); //EN Handle Mortality
void Death(); //EN Death
double getTimeToDeath(); //EN Return time to death
event timeDeathAtMaxLifespanEvent, DeathAtMaxLifespanEvent; //EN Death at max lifespan
event timeMortalityBaseEvent, MortalityBaseEvent; //EN Mortality event base model
event timeMortalityDetailedEvent, MortalityDetailedEvent; //EN Mortality event detailed model
};
actor Observer
{
Person_ptr GetNextToDie(Person_ptr prPerson); //EN Identify next person to die
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
TIME Person::timeDeathAtMaxLifespanEvent() { return time_of_birth + MAX(AGE_RANGE) + 0.99999; }
void Person::DeathAtMaxLifespanEvent() { Death(); }
void Person::Death()
{
is_alive = FALSE;
MaintainLinksAtDeath();
Finish();
}
void Person::HandleMortality()
{
if (SelectedMortalityModel != MOM_ALIGNED) Death(); // this person dies if no alignment
else lObserver->GetNextToDie(this)->Death(); // person to die to be found
}
TIME Person::timeMortalityBaseEvent()
{
TIME dEventTime = TIME_INFINITE;
double dMortalityHazard = MortalityTable[sex][integer_age][RANGE_POS(SIM_YEAR, calendar_year)];
// check if a person is at risk
if (in_projected_time && is_resident && dMortalityHazard > 0.0 && SelectedMortalityModel != MOM_DETAIL)
{
// determine the event time
dEventTime = WAIT(-log(RandUniform(14)) / dMortalityHazard);
}
return dEventTime;
}
void Person::MortalityBaseEvent()
{
HandleMortality();
}
TIME Person::timeMortalityDetailedEvent()
{
TIME tEventTime = TIME_INFINITE;
double dHazard = MortalityDetailedHazard[sex][educ_level3][integer_age][RANGE_POS(SIM_YEAR, calendar_year)];
if (in_projected_time && is_resident && dHazard > 0.0 && SelectedMortalityModel == MOM_DETAIL)
{
tEventTime = WAIT(-TIME(log(RandUniform(31)) / dHazard));
}
return tEventTime;
}
void Person::MortalityDetailedEvent()
{
HandleMortality();
}
double Person::getTimeToDeath()
{
double dWaitingTime = TIME_INFINITE;
double dHazard = MortalityDetailedHazard[sex][educ_level3][integer_age][RANGE_POS(SIM_YEAR, calendar_year)];
if (dHazard > 0.0) dWaitingTime = -log(RandUniform(32)) / dHazard;
return dWaitingTime;
}
Person_ptr Observer::GetNextToDie(Person_ptr prPers)
{
long nPopSize = asAllMortalPersonsForMortalityAlignment[prPers->sex][prPers->integer_age]->Count();
Person_ptr ptrNextDead = NULL;
double dWaitToDeath = TIME_INFINITE;
for (long nI = 0; nI < nPopSize; nI++)
{
Person_ptr ptrThisOne = asAllMortalPersonsForMortalityAlignment[prPers->sex][prPers->integer_age]->Item(nI);
double dThisWaitTime = ptrThisOne->getTimeToDeath();
if (dThisWaitTime <= dWaitToDeath)
{
dWaitToDeath = dThisWaitTime;
ptrNextDead = ptrThisOne;
}
}
return ptrNextDead;
}
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Pre-Simulation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void PreSimulation()
{
// Mortality rates by population group are found by binary search. For each simulated year, the overall mortality table
// is adjusted to obtain target life expectancies at age 65 and at age 25 for each distinguished population group.
// Local variables
double dTarget, dCenter, dResult, dAlive, dDeaths, dLower, dUpper;
int nIterations;
if (SelectedMortalityModel != MOM_BASE)
{
// Find trend factors to fit the life expectancy at 65
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
for (int nYear = 0; nYear < SIZE(SIM_YEAR); nYear++)
{
for (int nGroup = 0; nGroup < SIZE(EDUC_LEVEL3); nGroup++)
{
dTarget = LifeExpectancy[nSex][LE_65][nYear][nGroup]; // Target life expectancy
dResult = 0.0; // Search result: life expectancy
dLower = 0.01; // Lower limit of calibration factor
dUpper = 100.0; // Upper limit of calibration factor
nIterations = 100000; // Maximal iterations
while (abs(dResult - dTarget) > 0.0001 && nIterations > 0)
{
nIterations--;
dCenter = (dLower + dUpper) / 2.0; // New calibration factor for probing
dResult = 0.0;
dAlive = 1.0; // Proportion of people still alive
// Life expectancy calculated applying calibration factor
for (int nAge = 65; nAge < SIZE(AGE_RANGE); nAge++)
{
// proportion of deaths in year: survival = exp(-hazard)
dDeaths = dAlive * (1 - exp(-MortalityTable[nSex][nAge][nYear] * (1.0 + (dCenter - 1.0) * MortalityAdjustment[nSex][RANGE_POS(AGE_25P, nAge)][nGroup])));
dAlive = dAlive - dDeaths;
// people dying in this year are assumed to die in the middle of the year
dResult = dResult + dDeaths * 0.5 + dAlive;
}
// Moving the search limits for next iteration
if (dTarget < dResult) dLower = dCenter;
else dUpper = dCenter;
}
// applying the best solution to the mortality parameter
for (int nAge = 65; nAge < SIZE(AGE_RANGE); nAge++)
{
MortalityDetailedHazard[nSex][nGroup][nAge][nYear] = MortalityTable[nSex][nAge][nYear] * (1.0 + (dCenter - 1.0) * MortalityAdjustment[nSex][RANGE_POS(AGE_25P, nAge)][nGroup]);
}
}
}
}
// Find trend factors to fit the life expectancy at 25 (while keeping the trend for 65+)
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
for (int nYear = 0; nYear < SIZE(SIM_YEAR); nYear++)
{
for (int nGroup = 0; nGroup < SIZE(EDUC_LEVEL3); nGroup++)
{
dTarget = LifeExpectancy[nSex][LE_25][nYear][nGroup]; // Target life expectancy
dResult = 0.0; // Search result: life expectancy
dLower = 0.01; // Lower limit of calibration factor
dUpper = 100.0; // Upper limit of calibration factor
nIterations = 100000; // Maximal iterations
while (abs(dResult - dTarget) > 0.0001 && nIterations > 0)
{
nIterations--;
dCenter = (dLower + dUpper) / 2.0; // New calibration factor for probing
dResult = 0.0;
dAlive = 1.0; // Proportion of people still alive
// Life expectancy calculated applying calibration factor
for (int nAge = 25; nAge < SIZE(AGE_RANGE); nAge++)
{
// proportion of deaths in year: survival = exp(-hazard)
if (nAge < 65) // Apply searched adjustment factor only for ages below 65
{
dDeaths = dAlive * (1 - exp(-MortalityTable[nSex][nAge][nYear] * (1.0 + (dCenter - 1.0) * MortalityAdjustment[nSex][RANGE_POS(AGE_25P, nAge)][nGroup])));
}
else // apply known factor for ages 65+
{
dDeaths = dAlive * (1 - exp(-MortalityDetailedHazard[nSex][nGroup][nAge][nYear]));
}
dAlive = dAlive - dDeaths;
// people dying in this year are assumed to die in the middle of the year
dResult = dResult + dDeaths * 0.5 + dAlive;
}
// Moving the search limits for next iteration
if (dTarget < dResult) dLower = dCenter;
else dUpper = dCenter;
}
// applying the best solution to the mortality parameter
for (int nAge = 25; nAge < 65; nAge++)
{
MortalityDetailedHazard[nSex][nGroup][nAge][nYear] = MortalityTable[nSex][nAge][nYear] * (1.0 + (dCenter - 1.0) * MortalityAdjustment[nSex][RANGE_POS(AGE_25P, nAge)][nGroup]);
}
}
}
}
// Copy over parameters for age < 25
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
for (int nYear = 0; nYear < SIZE(SIM_YEAR); nYear++)
{
for (int nAge = 0; nAge < 25; nAge++)
{
for (int nGroup = 0; nGroup < SIZE(EDUC_LEVEL3); nGroup++)
{
MortalityDetailedHazard[nSex][nGroup][nAge][nYear] = MortalityTable[nSex][nAge][nYear];
}
}
}
}
}
}
Migration.mpp
The migration module handles net migration by age and sex, parameters typically taken from official (e.g. Eurostat) population projections. Immigrants are created by the simulation engine, their number and age distribution being calculated from the net migration parameter in the pre-simulation function in this module. Immigrants arrive at random times within a year. In contrast, emigration is modelled as occurring only once in the middle of each year. Emigration is handled by the Observer actor, the event implemented in this module. The migration module also initialises the educational and family characteristics of migrants and links migrant mothers to children arriving in the same year. The concept of net migration does not allow for the modelling of life course heterogeneity by place of origin, so immigrants are assumed to be no different from residents.
Like all other persons, immigrants are created at birth. Unlike residents, they are not subject to life course events such as mating or mortality until they immigrate. Instead, they acquire most of their characteristics by cloning from a resident host. This happens at two points in time:
At birth, babies sample their educational ‘destiny’ and their parents’ education from resident babies.
At the time of immigration, a resident host of the same age, sex and education is randomly selected and relevant characteristics are cloned. For women, this includes characteristics such as number of children and whether a first or second birth is currently expected. If a female host lives with dependent children, the corresponding female immigrant tries to find children of the same age in the pool of immigrants arriving in the same year (so far unattended). While this approach treats the fertility of immigrant women as similar to that of the resident population, it does not treat partnerships separately. All immigrants arrive as singles (including single mothers with dependent children) and, from the next mid-month event onwards, become subject to the periodic partnership updates treated in the partnerships module.
Parameters:
Migration On/Off
Number of net migrants by age, sex, and year
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN Unattended migrants
actor_set Person asUnattendedImmigrantChildren[integer_age]
filter is_alive && creation_type == CT_IMMIGRANT && is_unattended && immi_this_year;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG_MIGRATION //EN Migration
{
ModelMigration,
NetMigrationSexAgePeriod
};
parameters
{
logical ModelMigration; //EN Migration On/Off
double NetMigrationSexAgePeriod[SEX][AGE_RANGE][SIM_YEAR]; //EN Net migration by age and sex
model_generated double NumberImmigrants[SIM_YEAR][SEX]; //EN Number of immigrants
model_generated cumrate AgeImmigrants[SEX][SIM_YEAR][AGE_RANGE]; //EN Age distribution of immigrants
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
logical is_unattended = { FALSE }; //EN Unattended immigrant
//EN Scheduled to immigrate in this year
logical immi_this_year = (int(time_of_immigration) == calendar_year) ? TRUE : FALSE;
void setImmiEducAtBirth(); //EN Sample education from host at birth
void setImmiStatesAtImmigration(); //EN Sample states from host at immigration
void doEmigrate(); //EN Emigrate
TIME time_of_immigration = { TIME_INFINITE }; //EN Time of first immigration
event timeImmigrationEvent, ImmigrationEvent; //EN Immigration event
};
actor Observer
{
TIME next_emigration_event = { TIME_INFINITE }; //EN Next emigration event
event timeEmigrationEvent, EmigrationEvent; //EN Emigration event
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Person::doEmigrate()
{
is_resident = FALSE;
Death();
}
void Person::setImmiStatesAtImmigration()
{
logical bHostExists = FALSE;
if (asResidentsAgeSexEduc[integer_age][sex][educ_level3]->Count() > 0) bHostExists = TRUE;
// Female in reproductive age or above
if (sex == FEMALE && integer_age >= MIN(FERTILE_AGE) && !lives_with_mother && bHostExists)
{
Person_ptr ptrHost = asResidentsAgeSexEduc[integer_age][sex][educ_level3]->GetRandom(RandUniform(48));
number_children2 = ptrHost->number_children2;
waiting_for_first_birth = ptrHost->waiting_for_first_birth;
waiting_for_second_birth = ptrHost->waiting_for_second_birth;
ready_for_higher_birth = ptrHost->ready_for_higher_birth;
// loop through children in hosts family
int nIndex = 0;
Person_ptr ptrHostChild = ptrHost->mlRecentMotherChildren->GetNext(0, &nIndex);
while (ptrHostChild)
{
if (ptrHostChild->lives_with_mother)
{
integer nChildAge = ptrHostChild->integer_age;
if (asUnattendedImmigrantChildren[nChildAge]->Count() > 0)
{
Person_ptr ptrOwnChild = asUnattendedImmigrantChildren[nChildAge]->GetRandom(RandUniform(49));
ptrOwnChild->lFirstMother = (Person_ptr)this;
ptrOwnChild->lRecentMother = (Person_ptr)this;
ptrOwnChild->is_unattended = FALSE;
ptrOwnChild->lives_with_mother = TRUE;
}
}
// pointer to next child
ptrHostChild = ptrHost->mlRecentMotherChildren->GetNext(nIndex + 1, &nIndex);
}
// Set clock for time since first birth
if (number_children2 == NC2_1)
{
int nIndex = 0;
// Get the link to the child (there should only be one -- otherwise the first)
Person_ptr ptrChild = mlRecentMotherChildren->GetNext(0, &nIndex);
// If no child was found and linked: take time of birth of host child as proxy
if (!ptrChild)
{
ptrChild = ptrHost->mlRecentMotherChildren->GetNext(0, &nIndex);
}
// Now set the clock
if (ptrChild)
{
time_first_birth = ptrChild->time_of_birth;
double dTimeSinceFirstBirth = time - time_first_birth;
int nTimeSinceFirstBirth = int(dTimeSinceFirstBirth);
if (nTimeSinceFirstBirth <= MAX(FERT_PROG))
{
years_since_first_birth = nTimeSinceFirstBirth;
time_next_year_since_first_birth = WAIT(dTimeSinceFirstBirth - nTimeSinceFirstBirth);
}
else
{
years_since_first_birth = 99;
time_next_year_since_first_birth = TIME_INFINITE;
}
}
}
}
}
void Person::setImmiEducAtBirth()
{
EDUC_LEVEL4 cEduc = EL4_ISCED2;
PARENTS_EDUC cParEduc = PED_UNKNOWN;
if (asResidentsAgeSex[0][sex]->Count() > 0)
{
Person_ptr ptrBabyHost = asResidentsAgeSex[0][sex]->GetRandom(RandUniform(45));
cEduc = ptrBabyHost->educ_level4;
cParEduc = ptrBabyHost->parents_educ;
}
educ_level4 = cEduc;
parents_educ = cParEduc;
}
TIME Person::timeImmigrationEvent()
{
if (!is_resident) return time_of_immigration;
else return TIME_INFINITE;
}
void Person::ImmigrationEvent()
{
is_resident = TRUE;
setImmiStatesAtImmigration();
}
TIME Observer::timeEmigrationEvent() { return next_emigration_event; }
void Observer::EmigrationEvent()
{
// for each age by sex
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
for (int nAge = 0; nAge < SIZE(AGE_RANGE); nAge++)
{
double dExpectedEmigrants = 0.0;
long nExpectedEmigrants = 0;
if (NetMigrationSexAgePeriod[nSex][nAge][RANGE_POS(SIM_YEAR, observer_year)] < 0) // there is net emigration
{
// determine number of emigrants
dExpectedEmigrants = -NetMigrationSexAgePeriod[nSex][nAge][RANGE_POS(SIM_YEAR, observer_year)] / ScalingFactor;
nExpectedEmigrants = int(dExpectedEmigrants);
if (RandUniform(47) < dExpectedEmigrants - (double)nExpectedEmigrants) nExpectedEmigrants++;
// make somebody emigrate
for (int nIndex = 0; nIndex < nExpectedEmigrants; nIndex++)
{
if (asResidentsAgeSex[nAge][nSex]->Count() > 0)
{
Person_ptr prPerson = asResidentsAgeSex[nAge][nSex]->GetRandom(RandUniform(46));
prPerson->doEmigrate();
}
}
}
}
}
next_emigration_event = WAIT(1.0);
}
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Pre-Simulation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void PreSimulation()
{
// Initialize
for (int nYear = 0; nYear < SIZE(SIM_YEAR); nYear++)
{
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
NumberImmigrants[nYear][nSex] = 0.0;
}
}
// Net migration: Immigrants
if (ModelMigration)
{
for (int nYear = 0; nYear < SIZE(SIM_YEAR); nYear++)
{
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
double dSumImmigrants = 0;
for (int nAge = 0; nAge < SIZE(AGE_RANGE); nAge++)
{
if (NetMigrationSexAgePeriod[nSex][nAge][nYear] > 0)
{
AgeImmigrants[nSex][nYear][nAge] = NetMigrationSexAgePeriod[nSex][nAge][nYear];
dSumImmigrants = dSumImmigrants + NetMigrationSexAgePeriod[nSex][nAge][nYear];
}
else
{
AgeImmigrants[nSex][nYear][nAge] = 0.0;
}
}
NumberImmigrants[nYear][nSex] = dSumImmigrants;
}
}
}
}
Partnerships.mpp
This module implements processes for maintaining the partnership status of women over the life course (union formation, dissolution, matching a suitable partner). The female partnership status is updated monthly according to observed partnership patterns by education, age, and age of the youngest child.
The model maintains the patterns contained in the parameters. Thus we assume that these patterns are stable and changes in aggregate partnership characteristics only result from compositional changes in the female population like changes in the education composition, childlessness or timing of births. The model follows a ‘minimum necessary corrections’ approach changing the union status of women only to meet aggregate numbers. In reality, unions are more unstable, i.e. the model does not move women out of a union and others in if the aggregate proportion does not change. The current version is longitudinally consistent only on the cohort level by education and the number of children ever born (childless, one child, two or more children). Alignments can be switched off for higher ages (see below).
Partner matching is modelled by age and education. We model only two-sex couples. For age differences, we assume that the patterns of observed age differences in couples by age persist over time. One difficulty in assigning a partner is that the distribution of age differences changes with age at union formation. For example, a young man cannot have a much younger spouse (or vice versa), while the spread of observed age differences increases with age. As information on union formation and duration is usually not available in surveys and administrative data are only available for marriages, we follow an indirect approach based on the observed age patterns in existing partnerships. The algorithm is as follows:
Based on the distribution parameter of age differences between spouses, we calculate the expected number of partners by age for the age of the seeking woman in the simulation.
We then calculate the number of actual partners by age in the simulated population.
By comparing the expected and observed distributions, we identify the age with the largest negative gap for which there is at least one available male partner.
Having identified the pool of available partners, a second criterion is education, which is sampled from a distributional parameter. Current patterns are assumed to be persistent and maintainable over time.
Parameters:
Partnerships of women with dependent children: probability of being in a partnership by education, age group and age group of youngest child. This parameter is usually estimated from survey data such as SILC. These probabilities are assumed to remain constant in the future.
Partnerships of women not living with dependent children: probability of being in a partnership by education and age. This parameter is usually estimated from survey data such as SILC. These probabilities are assumed to remain constant in the future.
Highest age at union dissolution other than widowhood: This parameter makes it possible to switch off the adjustment to (lower) target rates. This is useful for creating scenarios that assume union stability at higher ages, where, due to improvements in mortality, it can be assumed that people stay in unions longer because of the increase in life expectancy of the partner.
Highest age at union formation: This parameter allows to switch off the adjustment to (higher) target rates. This is useful for sensitivity analysis, i.e. to create scenarios in which no new union formation occurs from a certain age.
Distribution of partner ages by age of female partner: This parameter is usually estimated from survey data such as SILC. It is assumed that these distributions will remain constant in the future.
Distribution of partner’s education by education level of female partner. This parameter is usually based on educational patterns of currently young couples, estimated from survey data such as SILC, It is assumed that these distributions will remain constant in the future.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN Women living with dependent children
actor_set Person asWomenWithChildren[educ_level3][child_agegr][moth_agegr][has_spouse]
filter is_alive && is_resident && in_projected_time && sex == FEMALE && WITHIN(SPOUSE_AGE, integer_age) &&
children_in_family > 0 && !is_blocked_from_marriage;
//EN Women not living with dependent children
actor_set Person asWomenNoChildren[educ_level3][partnership_age][has_spouse]
filter is_alive && is_resident && in_projected_time && sex == FEMALE && WITHIN(SPOUSE_AGE, integer_age) &&
children_in_family == 0 && !is_blocked_from_marriage;
//EN Potential male spouses by age and education
actor_set Person asAvailableMaleForPartnership[partnership_age][educ_level3]
filter is_alive && is_resident && in_projected_time && sex == MALE && !has_spouse && WITHIN(SPOUSE_AGE, integer_age);
//EN Women in a partnership by own and partner's age
actor_set Person asFemaleInPartnershipByAgeAndPartnerAge[partnership_age][partnership_spouse_age]
filter is_alive && is_resident && in_projected_time && sex == FEMALE && has_spouse && WITHIN(SPOUSE_AGE, integer_age);
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
range SPOUSE_AGE { 15, 105 }; //EN Age
partition CHILD_AGEGR_PART { 1, 3, 6, 9, 12, 15 }; //EN Age of youngest child
partition MOTH_AGEGR_PART { 20, 25, 30, 35, 40 }; //EN Age of mother at last birth
classification MOTH_AGEGR //EN Age group mothers at birth
{
MOA_20, //EN Below 20
MOA_25, //EN 20 to 24
MOA_30, //EN 25 to 19
MOA_35, //EN 30 to 34
MOA_40, //EN 35 to 39
MOA_40P //EN 40+
};
classification CHILD_AGEGR //EN Age group child
{
CHA_00, //EN 0
CHA_01, //EN 1 to 2
CHA_03, //EN 3 to 5
CHA_06, //EN 6 to 8
CHA_09, //EN 9 to 11
CHA_12, //EN 12 to 14
CHA_15 //EN 15 to 17
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG07_FemalePartnerships //EN Partnerships
{
InUnionProbWithChildren,
InUnionProbNoChildren,
MaxAgePartnershipFormationAlignment,
MaxAgePartnershipDissolutionAlignment,
ProbStayWithMother,
PartnerAgeDistribution,
PartnerEducDistribution
};
parameters
{
//EN Probability to be in a partnership - Females living with children
double InUnionProbWithChildren[EDUC_LEVEL3][CHILD_AGEGR][MOTH_AGEGR];
//EN Probability to be in a partnership - Females not living with children
double InUnionProbNoChildren[SPOUSE_AGE][EDUC_LEVEL3];
//EN Max age partnership formation alignment
double MaxAgePartnershipFormationAlignment;
//EN Max age partnership dissolution alignment
double MaxAgePartnershipDissolutionAlignment;
//EN Distribution of partner ages by age of female partner
double PartnerAgeDistribution[SPOUSE_AGE][SPOUSE_AGE];
//EN Distribution of partner characteristics by female characteristics
cumrate PartnerEducDistribution[EDUC_LEVEL3][EDUC_LEVEL3];
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
//EN Age at last birth
double age_last_birth = (sex == FEMALE && children_in_family > 0) ?
integer_age - age_youngest_child_in_family : TIME_INFINITE;
//EN Age group of youngest child of women
int child_agegr_part = split(age_youngest_child_in_family, CHILD_AGEGR_PART);
//EN Age group at last birth
int moth_agegr_part = split(age_last_birth, MOTH_AGEGR_PART);
//EN Age group at last birth
MOTH_AGEGR moth_agegr = (moth_agegr_part == 0) ? MOA_20 :
(moth_agegr_part == 1) ? MOA_25 :
(moth_agegr_part == 2) ? MOA_30 :
(moth_agegr_part == 3) ? MOA_35 :
(moth_agegr_part == 4) ? MOA_40 : MOA_40P;
//EN Age group child
CHILD_AGEGR child_agegr = (child_agegr_part == 0) ? CHA_00 :
(child_agegr_part == 1) ? CHA_01 :
(child_agegr_part == 2) ? CHA_03 :
(child_agegr_part == 3) ? CHA_06 :
(child_agegr_part == 4) ? CHA_09 :
(child_agegr_part == 5) ? CHA_12 : CHA_15;
//EN Age
SPOUSE_AGE partnership_age = COERCE(SPOUSE_AGE, integer_age);
//EN Age of partner
SPOUSE_AGE partnership_spouse_age = (has_spouse) ? COERCE(SPOUSE_AGE, lSpouse->integer_age) : MAX(SPOUSE_AGE);
logical is_blocked_from_marriage = { FALSE }; //EN Blocked from marriage
logical FindSpouse(); //EN Find and link spouse
};
actor Observer
{
void UpdatePartnershipStatus(); //EN Update Female Partnership Status
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Observer::UpdatePartnershipStatus()
{
long nTarget;
if (observer_year >= MIN(SIM_YEAR))
{
// unblock all
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++) asAllPerson->Item(nJ)->is_blocked_from_marriage = FALSE;
// Women with children
for (int nGroup = 0; nGroup < SIZE(EDUC_LEVEL3); nGroup++)
{
for (int nChildAge = 0; nChildAge < SIZE(CHILD_AGEGR); nChildAge++)
{
for (int nMothAge = 0; nMothAge < SIZE(MOTH_AGEGR); nMothAge++)
{
long nGroupSize = asWomenWithChildren[nGroup][nChildAge][nMothAge][FALSE]->Count()
+ asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->Count();
nTarget = round(InUnionProbWithChildren[nGroup][nChildAge][nMothAge] * nGroupSize);
if (nTarget > asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->Count())
{
// move some into partnership until target met
while (nTarget > asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->Count() &&
asWomenWithChildren[nGroup][nChildAge][nMothAge][FALSE]->Count() > 0)
{
auto prFam = asWomenWithChildren[nGroup][nChildAge][nMothAge][FALSE]->GetRandom(RandUniform(4));
if (!prFam->FindSpouse()) prFam->is_blocked_from_marriage = TRUE;
}
}
else if (nTarget < asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->Count())
{
while (nTarget < asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->Count() &&
asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->Count() > 0)
{
auto prFam = asWomenWithChildren[nGroup][nChildAge][nMothAge][TRUE]->GetRandom(RandUniform(33));
prFam->DissolvePartnership();
}
}
}
}
}
//Targets for women without children in hh
for (int nGroup = 0; nGroup < SIZE(EDUC_LEVEL3); nGroup++)
{
for (int nAge = 0; nAge < SIZE(SPOUSE_AGE); nAge++)
{
nTarget = round(InUnionProbNoChildren[nAge][nGroup]
* (asWomenNoChildren[nGroup][nAge][FALSE]->Count() + asWomenNoChildren[nGroup][nAge][TRUE]->Count()));
if (nTarget > asWomenNoChildren[nGroup][nAge][TRUE]->Count() && MIN(SPOUSE_AGE) + nAge <= MaxAgePartnershipFormationAlignment)
{
// move some into marriage until target met
while (nTarget > asWomenNoChildren[nGroup][nAge][TRUE]->Count() &&
asWomenNoChildren[nGroup][nAge][FALSE]->Count() > 0)
{
auto prFam = asWomenNoChildren[nGroup][nAge][FALSE]->GetRandom(RandUniform(58));
if (!prFam->FindSpouse()) prFam->is_blocked_from_marriage = TRUE;
}
}
else if (nTarget < asWomenNoChildren[nGroup][nAge][TRUE]->Count() && MIN(SPOUSE_AGE) + nAge <= MaxAgePartnershipDissolutionAlignment)
{
while (nTarget < asWomenNoChildren[nGroup][nAge][TRUE]->Count() &&
asWomenNoChildren[nGroup][nAge][TRUE]->Count() > 0)
{
auto prFam = asWomenNoChildren[nGroup][nAge][TRUE]->GetRandom(RandUniform(39));
prFam->DissolvePartnership();
}
}
}
}
}
}
logical Person::FindSpouse()
{
bool bFoundSpouse = FALSE;
double dExpectedPartners[SIZE(SPOUSE_AGE)];
double dObservedPartners[SIZE(SPOUSE_AGE)];
double dSumExpectedPartners = 0;
double dSumObservedPartners = 0;
double dGap = 0.0;
double dLargestGap = 0.0;
int nAgePartner;
int nEducPartner;
Person_ptr ptrSpouse = NULL;
// Partner age
// Totals in distributional tables
for (int nAge = 0; nAge < SIZE(SPOUSE_AGE); nAge++)
{
dExpectedPartners[nAge] = PartnerAgeDistribution[RANGE_POS(SPOUSE_AGE, integer_age)][nAge];
dObservedPartners[nAge] = asFemaleInPartnershipByAgeAndPartnerAge[RANGE_POS(SPOUSE_AGE, integer_age)][nAge]->Count();
dSumExpectedPartners = dSumExpectedPartners + dExpectedPartners[nAge];
dSumObservedPartners = dSumObservedPartners + dObservedPartners[nAge];
}
// Standardize distributions
for (int nAge = 0; nAge < SIZE(SPOUSE_AGE); nAge++)
{
if (dSumExpectedPartners == 0.0) dSumExpectedPartners = 1.0;
if (dSumObservedPartners == 0.0) dSumObservedPartners = 1.0;
dExpectedPartners[nAge] = dExpectedPartners[nAge] / dSumExpectedPartners;
dObservedPartners[nAge] = dObservedPartners[nAge] / dSumObservedPartners;
}
// Find age with largest gap comparing distributions
for (int nAge = 0; nAge < SIZE(SPOUSE_AGE); nAge++)
{
dGap = dExpectedPartners[nAge] - dObservedPartners[nAge];
int nAvailableSpouses = asAvailableMaleForPartnership[nAge][EL3_LOW]->Count()
+ asAvailableMaleForPartnership[nAge][EL3_MEDIUM]->Count()
+ asAvailableMaleForPartnership[nAge][EL3_HIGH]->Count();
if (dExpectedPartners[nAge] > 0.0 && dGap >= dLargestGap && nAvailableSpouses > 0)
{
dLargestGap = dGap;
bFoundSpouse = TRUE;
nAgePartner = MIN(SPOUSE_AGE) + nAge;
}
}
// Partner Education
int ecode = 0;
if (bFoundSpouse)
{
Lookup_PartnerEducDistribution(RandUniform(40), educ_level3, &nEducPartner);
// Look if somebody with desired characteristics is available
if (asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][nEducPartner]->Count() > 0)
{
ptrSpouse = asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][nEducPartner]->GetRandom(RandUniform(36));
}
// Else take somebody with target age only - this should be rarely the case
else if (asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][EL3_LOW]->Count() > 0)
{
ptrSpouse = asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][EL3_LOW]->GetRandom(RandUniform(35));
}
else if (asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][EL3_MEDIUM]->Count() > 0)
{
ptrSpouse = asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][EL3_MEDIUM]->GetRandom(RandUniform(37));
}
else if (asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][EL3_HIGH]->Count() > 0)
{
ptrSpouse = asAvailableMaleForPartnership[RANGE_POS(SPOUSE_AGE, nAgePartner)][EL3_HIGH]->GetRandom(RandUniform(38));
}
else bFoundSpouse = FALSE;
}
// Start the partnership
if (bFoundSpouse) StartPartnership(ptrSpouse);
// Return success
return bFoundSpouse;
}
Family.mpp
The family module manages and maintains family relationships. MicroWELT follows a nuclear family concept, where families consist of a household head and - if present - a spouse and dependent children. Accordingly, each person has a family role, which can be head, spouse or child. The female spouse is considered to be the head of the family. The model distinguishes three types of links, namely links between spouses, links to ‘first’ parents (biological or first known mothers and fathers as observed in the starting population) and links to the most ‘recent’ parents, e.g. stepparents. Links to parents are maintained throughout life; ‘recent’ parents are the last biological or social parents with whom a child lived before leaving home. Information about whether a person still lives with his or her mother and/or father is maintained in a logical state.
The module contains a collection of functions that handle links at specific life history events:
Death: If there is no spouse but children in the family, each child checks whether it has a biological mother or father or a grandmother or grandfather still alive, in which case the child links to a new guardian (and - if present - to the spouse of this new social parent).
Partnerip formation: Partners are linked and form a new nuclear family. All children update their family links.
Dissolution of the union: Before the union between partners is dissolved, all children have to choose with whom they want to live. The choice is modelled by a set of simple rules and a probability to stay with the mother. If only one of the two parents is a biological parent, the children choose to stay with the biological parent. Otherwise, the choice is random, depending on the probability parameter.
Initial family ties of persons in the initial population: Links between spouses and to mothers and fathers; the observed parents are assumed to be the ‘first’ as well as the ‘recent’ parents.
Parameters:
Probability of living with mother after dissolution of parental partnership
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Family Links
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
link Person.lFirstFather Person.mlFirstFatherChildren[]; //EN First father - children
link Person.lFirstMother Person.mlFirstMotherChildren[]; //EN First mother - children
link Person.lRecentFather Person.mlRecentFatherChildren[]; //EN Most recent father - children
link Person.lRecentMother Person.mlRecentMotherChildren[]; //EN Most recent mother - children
link Person.lSpouse; //EN Link to spouse
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification FAMILY_ROLE //EN Family role
{
FR_HEAD, //EN Head
FR_SPOUSE, //EN Spouse
FR_CHILD //EN Child
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameters
{
//EN Probability to stay with mother after partnership disslolution
double ProbStayWithMother;
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
// Simple states
logical lives_with_father = { FALSE }; //EN Lives with father
logical lives_with_mother = { FALSE }; //EN Lives with mother
// Derived states
//EN Lives with parents
logical lives_with_parents = (lives_with_father || lives_with_mother) ? TRUE : FALSE;
//EN Lives with two parents
logical lives_with_two_parents = (lives_with_father && lives_with_mother) ? TRUE : FALSE;
//EN Has spouse
logical has_spouse = (lSpouse) ? TRUE : FALSE;
//EN Family role
FAMILY_ROLE family_role = (lSpouse && sex == MALE) ? FR_SPOUSE :
(lives_with_parents) ? FR_CHILD : FR_HEAD;
//EN Children in Family
short children_in_family = (sex == FEMALE) ?
sum_over(mlRecentMotherChildren, lives_with_mother) :
sum_over(mlRecentFatherChildren, lives_with_father);
//EN Time of birth oldest child in family
double tob_oldest_child_in_family =
(sex == FEMALE && children_in_family > 0) ? double(min_over(mlRecentMotherChildren, time_of_birth)) :
(sex == MALE && children_in_family > 0) ? double(min_over(mlRecentFatherChildren, time_of_birth)) : double(TIME_INFINITE);
//EN Youngest child in family
int age_youngest_child_in_family =
(sex == FEMALE && children_in_family > 0) ? double(min_over(mlRecentMotherChildren, integer_age)) :
(sex == MALE && children_in_family > 0) ? double(min_over(mlRecentFatherChildren, integer_age)) : TIME_INFINITE;
// Functions
void LinkToFamilyWhenSetAlive(); //EN Link family members
void StartPartnership(Person_ptr ptrSpouse); //EN Start partnership
void DissolvePartnership(); //EN Dissolve partnership
void MaintainLinksAtDeath(); //EN Maintain links at death
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Person::StartPartnership(Person_ptr ptrSpouse)
{
// link to partner
lSpouse = ptrSpouse;
// Partners children in family now live also with this woman
if (lSpouse->children_in_family > 0)
{
int nIndex = 0;
auto prChild = lSpouse->mlRecentFatherChildren->GetNext(0, &nIndex);
while (prChild)
{
if (prChild->lives_with_father)
{
prChild->lRecentMother = this;
prChild->lives_with_mother = TRUE;
}
prChild = lSpouse->mlRecentFatherChildren->GetNext(nIndex + 1, &nIndex);
}
}
// Own children in family now live also with this spouse
if (children_in_family > 0)
{
int nIndex;
auto prChild = mlRecentMotherChildren->GetNext(0, &nIndex);
while (prChild)
{
if (prChild->lives_with_mother)
{
// add only new children
if (!prChild->lRecentFather || (prChild->lRecentFather && (Person_ptr)prChild->lRecentFather != (Person_ptr)lSpouse))
{
prChild->lRecentFather = lSpouse;
prChild->lives_with_father = TRUE;
}
}
prChild = mlRecentMotherChildren->GetNext(nIndex + 1, &nIndex);
}
}
}
void Person::DissolvePartnership()
{
// Children deciding with whom to stay
if (children_in_family > 0)
{
int nIndex = 0;
bool bStayWithMother = (RandUniform(34) < ProbStayWithMother);
// Child decides to stay with mother
Person_ptr prChild = mlRecentMotherChildren->GetNext(0, &nIndex);
while (prChild)
{
if (
// only process children still living with their social mother
bStayWithMother && prChild->lives_with_mother
// and only cases where this mother is the biological mother
&& ((prChild->lFirstMother && (Person_ptr)prChild->lFirstMother == (Person_ptr)this)
// or the child does not know her biological father
|| !prChild->lFirstFather
// or the biologicl father is not the current social father
|| (prChild->lFirstFather && (Person_ptr)prChild->lFirstFather != (Person_ptr)lSpouse))
)
{
prChild->lives_with_father = FALSE;
}
prChild = mlRecentMotherChildren->GetNext(nIndex + 1, &nIndex);
}
// Those staying with social father stop living with their social mother
if (lSpouse->children_in_family > 0)
{
Person_ptr prChild = lSpouse->mlRecentFatherChildren->GetNext(0, &nIndex);
while (prChild)
{
if (prChild->lives_with_father) prChild->lives_with_mother = FALSE;
prChild = lSpouse->mlRecentFatherChildren->GetNext(nIndex + 1, &nIndex);
}
}
}
// Dissolve link to spouse
lSpouse = NULL;
}
void Person::MaintainLinksAtDeath()
{
int nIndex;
// Deceased person was a lone parent
if (!lSpouse && children_in_family > 0)
{
//try to find a guardian for children
Person_ptr prGuardian;
auto prChild = (sex == FEMALE) ? mlRecentMotherChildren->GetNext(0, &nIndex) : mlRecentFatherChildren->GetNext(0, &nIndex);
while (prChild)
{
if ((sex == FEMALE && prChild->lives_with_mother) || (sex == MALE && prChild->lives_with_father))
{
// Not living with deceased parent anymore
if (sex == FEMALE && prChild->lives_with_mother) prChild->lives_with_mother = FALSE;
else if (sex == MALE && prChild->lives_with_father) prChild->lives_with_father = FALSE;
// Try to identify a potential guardian
if (sex == FEMALE && prChild->lFirstFather) prGuardian = prChild->lFirstFather; // own biological father
else if (sex == MALE && prChild->lFirstMother) prGuardian = prChild->lFirstMother; // own biological mother
else if (lFirstMother) prGuardian = lFirstMother; // grandmother
else if (lFirstFather) prGuardian = lFirstFather; // grandfather
else prGuardian = NULL; // nobody found
// If somebody found link to this person - and, if available - the spouse of this person
if (prGuardian && prGuardian->sex == MALE)
{
prChild->lRecentFather = prGuardian;
prChild->lives_with_father = TRUE;
if (prGuardian->lSpouse)
{
prChild->lRecentMother = prGuardian->lSpouse;
prChild->lives_with_mother = TRUE;
}
}
else if (prGuardian && prGuardian->sex == FEMALE)
{
prChild->lRecentMother = prGuardian;
prChild->lives_with_mother = TRUE;
if (prGuardian->lSpouse)
{
prChild->lRecentFather = prGuardian->lSpouse;
prChild->lives_with_father = TRUE;
}
}
}
// set pointer to next child
prChild = (sex == FEMALE) ? mlRecentMotherChildren->GetNext(nIndex + 1, &nIndex) : mlRecentFatherChildren->GetNext(nIndex + 1, &nIndex);
}
}
// Deceased person was a parent in a partnership
else if (children_in_family > 0)
{
auto prChild = (sex == FEMALE) ? mlRecentMotherChildren->GetNext(0, &nIndex) : mlRecentFatherChildren->GetNext(0, &nIndex);
while (prChild)
{
// Not living with deceased parent anymore
if (sex == FEMALE && prChild->lives_with_mother) prChild->lives_with_mother = FALSE;
else if (sex == MALE && prChild->lives_with_father) prChild->lives_with_father = FALSE;
// set pointer to next child
prChild = (sex == FEMALE) ? mlRecentMotherChildren->GetNext(nIndex + 1, &nIndex) : mlRecentFatherChildren->GetNext(nIndex + 1, &nIndex);
}
}
}
void Person::LinkToFamilyWhenSetAlive()
{
// Family members from starting population
if (creation_type == CT_START && ptr_creator)
{
// Spouse
if (family_role_start == FR_HEAD || family_role_start == FR_SPOUSE) lSpouse = ptr_creator;
// Child
else if (family_role_start == FR_CHILD && ptr_creator->sex == MALE)
{
lRecentFather = ptr_creator;
lFirstFather = ptr_creator;
lives_with_father = TRUE;
if (lFirstFather->lSpouse)
{
lRecentMother = lFirstFather->lSpouse;
lFirstMother = lFirstFather->lSpouse;
lives_with_mother = TRUE;
}
}
else if (family_role_start == FR_CHILD && ptr_creator->sex == FEMALE)
{
lRecentMother = ptr_creator;
lFirstMother = ptr_creator;
lives_with_mother = TRUE;
if (lFirstMother->lSpouse)
{
lRecentFather = lFirstMother->lSpouse;
lFirstFather = lFirstMother->lSpouse;
lives_with_father = TRUE;
}
}
}
// Person born in simulation
else if (creation_type == CT_CHILD)
{
lRecentMother = ptr_creator;
lFirstMother = ptr_creator;
lives_with_mother = TRUE;
if (lFirstMother->lSpouse)
{
lRecentFather = lFirstMother->lSpouse;
lFirstFather = lFirstMother->lSpouse;
lives_with_father = TRUE;
// Fathers parity
if (lRecentFather->number_children2 == NC2_0) lRecentFather->number_children2 = NC2_1;
else if (lRecentFather->number_children2 == NC2_1) lRecentFather->number_children2 = NC2_2P;
}
}
}
MaleFamily.mpp
The modelling of family formation and dissolution in microWELT is female-driven, with males selected by assortative mating, taking into account age and education. Accordingly, male parity is updated with the birth of children by a partner. As only current partnerships and dependent children in the household can be observed in the starting population, information on other children is missing. This is taken into account by the following assumptions and approaches:
For men in the starting population living in a partnership, they are assumed to have the same number of children as their partner. This includes the imputed information on the number of children modelled in the fertility module (children who have already left home).
Male childlessness by education is modelled by a cohort parameter. To achieve this target childlessness, at the start of the simulation a proportion of currently childless men are flagged as never becoming fathers. If they become parents during the simulation, the flag is passed on to an unflagged childless man of the same age and education. During the simulation, flags are set at birth.
Single men aged 65+ at the start of the simulation who are not flagged as never becoming fathers are assumed to be fathers. Similarly, men who are not flagged as never becoming fathers when they turn 65 in the simulation are assumed to be fathers. This addresses a potential mismatch between the female-driven family dynamics and the male childlessness parameter and should affect only few people in the simulation. (No such correction is made if too many men are fathers at age 65 relative to the childlessness parameter). In all these cases of imputed fatherhood, the number of children (one versus 2 and more) is randomly decided on the basis of a parameter for the parity progression to the second child.
Parameters:
Male cohort childlessness by education
Male parity progression to second child used for imputation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Actor Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN Men of startpop by year of birth education and fatherhood
actor_set Person asMenStartpopYobEducFather[yob_past][educ_level3][never_father]
filter is_alive && creation_type == CT_START && sex == MALE;
//EN Men by year of birth and education who can be flagged as never father
actor_set Person asMenWhoCanBeFlaggedNeverFather[year_of_birth][educ_level3]
filter is_alive && is_resident && sex == MALE && !never_father && !known_father;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG_MALEFAMILY //EN Male family
{
MaleChildlessness,
MaleParityProgressionToSecondChild
};
parameters
{
double MaleChildlessness[ALL_YEAR][EDUC_LEVEL3]; //EN Male cohort childlessness
double MaleParityProgressionToSecondChild; //EN Male parity progression 2nd child for imputation
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
logical never_father = { FALSE }; //EN Destined never becoming father
logical known_father = { FALSE }; //EN Known father
YOB_PAST yob_past = COERCE(YOB_PAST, year_of_birth); //EN Year of birth
void setMaleLifetimeChildlessnessAtBirth(); //EN Assign lifetime childlessness at birth
void setMissingMaleParityAt65(); //EN Assign male parity at 65 if not observed
event timeChangeNeverFatherFlagEvent, ChangeNeverFatherFlagEvent; //EN Change never father flagging
};
actor Observer
{
void ImputeMaleParity(); //EN Impute male parity at start of simulation
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
TIME Person::timeChangeNeverFatherFlagEvent()
{
if (in_projected_time && is_resident && sex == MALE && never_father && children_in_family > 0) return WAIT(0.0);
else return TIME_INFINITE;
}
void Person::ChangeNeverFatherFlagEvent()
{
// Update states
never_father = FALSE;
known_father = TRUE;
// Find anotherone to overtake never-father flag
if (asMenWhoCanBeFlaggedNeverFather[RANGE_POS(ALL_YEAR, year_of_birth)][educ_level3]->Count() > 0)
{
Person_ptr ptrPerson = asMenWhoCanBeFlaggedNeverFather[RANGE_POS(ALL_YEAR, year_of_birth)][educ_level3]->GetRandom(RandUniform(51));
ptrPerson->never_father = TRUE;
}
}
void Person::setMaleLifetimeChildlessnessAtBirth()
{
if (RandUniform(24) < MaleChildlessness[RANGE_POS(ALL_YEAR, year_of_birth)][educ_level3]) never_father = TRUE;
else never_father = FALSE;
}
void Observer::ImputeMaleParity()
{
// Check own family links and inherit parity of female spouse
int nPersons = asAllPerson->Count();
for (int nIndex = 0; nIndex < nPersons; nIndex++)
{
Person_ptr prPerson = asAllPerson->Item(nIndex);
if (prPerson->sex == MALE && prPerson->is_resident)
{
if (prPerson->has_spouse) prPerson->number_children2 = prPerson->lSpouse->number_children2;
if (prPerson->number_children2 != NC2_0) prPerson->known_father = TRUE;
}
}
// Set flag for never father to meet external targets
for (int nYob = 0; nYob < SIZE(YOB_PAST); nYob++)
{
for (int nEduc = 0; nEduc < SIZE(EDUC_LEVEL3); nEduc++)
{
int nNeverFather = asMenStartpopYobEducFather[nYob][nEduc][TRUE]->Count();
int nEverFather = asMenStartpopYobEducFather[nYob][nEduc][FALSE]->Count();
int nExpectedNeverFather = int((nNeverFather + nEverFather) * MaleChildlessness[nYob][nEduc]);
while (nExpectedNeverFather > nNeverFather && asMenWhoCanBeFlaggedNeverFather[nYob][nEduc]->Count() > 0)
{
Person_ptr ptrPerson = asMenWhoCanBeFlaggedNeverFather[nYob][nEduc]->GetRandom(RandUniform(50));
ptrPerson->never_father = TRUE;
nNeverFather++;
}
}
}
// For men 65+ who are not in a partnership, use never_father flag to assign family size
int nPerson = asAllPerson->Count();
for (int nJ = 0; nJ < nPerson; nJ++)
{
Person_ptr paPerson = asAllPerson->Item(nJ);
if (paPerson->is_resident && paPerson->sex == MALE && paPerson->integer_age >= 65 && !paPerson->has_spouse && !paPerson->never_father)
{
if (RandUniform(52) < MaleParityProgressionToSecondChild) paPerson->number_children2 = NC2_2P;
else paPerson->number_children2 = NC2_1;
paPerson->known_father = TRUE;
}
}
}
void Person::setMissingMaleParityAt65()
{
if (!known_father && !never_father)
{
if (RandUniform(53) < MaleParityProgressionToSecondChild) number_children2 = NC2_2P;
else number_children2 = NC2_1;
known_father = TRUE;
}
}
LeavingHome.mpp
The module on leaving home deals with the economic emancipation of children. In the current implementation of the model, children leave home at the age of 18, or when they form their own nuclear family through union formation, or when they give birth.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
event timeLeavingHomeEvent, LeavingHomeEvent; //EN Leaving home
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
TIME Person::timeLeavingHomeEvent()
{
if ((lives_with_parents || is_unattended ) && (integer_age >= 18 || has_spouse || children_in_family > 0)) return WAIT(0.0);
else return TIME_INFINITE;
}
void Person::LeavingHomeEvent()
{
lives_with_mother = FALSE;
lives_with_father = FALSE;
is_unattended = FALSE;
}
ParentsEducation.mpp
Parental education is used to model the intergenerational transmission of education. It refers to the highest educational attainment of both parents. Parental education can be at one of three levels - low (ISCED 2 and below), medium (ISCED 3 and 4), high (ISCED 5 and above) - or unknown. Modelling the educational ‘destiny’ of a child requires knowledge of the educational composition of the parents of the child’s birth cohort, as odds ratios based on parental education need to be taken into account, while at the same time meeting outcome targets regarding the educational distribution of the child’s birth cohort.
Parental education is initialised at birth. Information on the current educational distribution of parents is provided by an observer function that tracks and allows retrieval of this distribution information based on the past 12 months, updated at each birth.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification PARENTS_EDUC //EN Parents education
{
PED_LOW, //EN Low
PED_MEDIUM, //EN Medium
PED_HIGH, //EN High
PED_UNKNOWN //EN Unknown
};
classification PARENTS_EDUC3 //EN Parents education
{
PE3_LOW, //EN Low
PE3_MEDIUM, //EN Medium
PE3_HIGH //EN High
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
PARENTS_EDUC parents_educ = { PED_UNKNOWN }; //EN Parents education
void setParentsEducAtBirth(); //EN Set parents education
};
actor Observer
{
int parents_educ_array[ALL_MONTH][PARENTS_EDUC]; //EN Array of parents education distribution
void doInitParentsEducArray(); //EN Initialise parents educatipn array
void doAddBirthToEducArray(PARENTS_EDUC cEduc); //EN Add a birth to the array
double getShareParentsEduc(PARENTS_EDUC cEduc); //EN Share of parents with education cEduc
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void Observer::doInitParentsEducArray()
{
for (int nMonth = 0; nMonth < SIZE(ALL_MONTH); nMonth++)
{
for (int nEduc = 0; nEduc < SIZE(PARENTS_EDUC); nEduc++)
{
parents_educ_array[nMonth][nEduc] = 0;
}
}
};
void Observer::doAddBirthToEducArray(PARENTS_EDUC cEduc)
{
int nMonth = int((time - MIN(ALL_YEAR)) * 12.0);
parents_educ_array[nMonth][cEduc] = parents_educ_array[nMonth][cEduc] + 1;
}
double Observer::getShareParentsEduc(PARENTS_EDUC cEduc)
{
double dReturnValue = 0.0;
double dSelected = 0.0;
double dAll = 0.0;
int nMonth = int((time - MIN(ALL_YEAR)) * 12.0);
for (int nPeriod = nMonth - 12; nPeriod < nMonth && nPeriod >= 0; nPeriod++)
{
for (int nEduc = 0; nEduc < SIZE(PARENTS_EDUC); nEduc++)
{
if (nEduc == (int)cEduc) dSelected = dSelected + parents_educ_array[nPeriod][cEduc];
if (cEduc == PED_UNKNOWN || (PARENTS_EDUC)nEduc != PED_UNKNOWN)
{
dAll = dAll + parents_educ_array[nPeriod][(PARENTS_EDUC)nEduc];
}
}
}
if (dAll > 0.0) dReturnValue = dSelected / dAll;
return dReturnValue;
}
void Person::setParentsEducAtBirth()
{
// set parents education
int nEduc = 0;
if (lFirstFather) nEduc = (int)lFirstFather->educ_level3;
if (lFirstMother)
{
if ((int)lFirstMother->educ_level3 > nEduc) nEduc = lFirstMother->educ_level3;
}
if (lFirstFather || lFirstMother) parents_educ = PARENTS_EDUC(nEduc);
else parents_educ = PED_UNKNOWN;
// store in matrix for distributional information
if (creation_type == CT_START || creation_type == CT_CHILD)
{
lObserver->doAddBirthToEducArray(parents_educ);
}
}
Education.mpp
The education module deals with “first chance” education, i.e. the first uninterrupted school career, which can lead to four different levels of education. The individual educational “destiny” is decided at birth. Gender and cohort specific outcome distributions can be specified by parameters. In addition, the model allows the specification of relative differences in educational attainment by parental education (intergenerational transmission of education, parameterised by odds ratios). In this way, for a given cohort’s educational distribution, parental background is taken into account when deciding who will receive which education. This alignment to cohort targets can also be switched off from a given point in time, after which educational change is driven entirely by the changing educational composition of the parents’ generation. For individuals in the initial population, the educational information on attendance and attainment from the starting population file is respected:
Older cohorts (born before 1990; the cut-off is set in the Context module) retain the same education as in the starting population.
Younger cohorts (born after 2000; the cut-off is set in the Context module) have their educational trajectories (re)assigned on the basis of the model parameters.
For intermediate cohorts, educational information from the starting population (school attendance, current highest level of education) is used, but higher levels of education can still be achieved by those who are enrolled in education. The model attempts to simultaneously respect the information from the starting population and meet the cohort targets set in the parameters. This is achieved through a combination of sampling and storage/retrieval of educational attainment. If a sampled education does not match the individual’s starting population information, it is stored in an array maintained by the observer and sampling is repeated. If the array is not empty, persons first check whether it contains an educational outcome that matches the individual characteristics of the starting population record.
Within the simulation, information on educational outcome targets and relative differences by parental education, together with the educational composition of parents, is used to determine individual progression rates consistent with the targets. This is achieved by numerical simulation (binary search for base odds which, when combined with odds ratios by parental education, give the target probabilities for the parental education distribution at that point in time). The distribution of parental education is derived within the simulation on the basis of births in the last 12 months. The information on births by parental education and month is maintained by the observer.
Parameters:
The distribution of educational attainment (4 levels) by cohort and gender. The levels are ISCED 2 or lower, ISCED 3, ISCED 4, and ISCED 5 or higher.
Odds ratios by sex and parental education (3 levels; ISCED 3 and 4 are combined) for each transition between school levels.
The (first) year from which educational attainment by gender and parental education is fixed. This parameter makes it possible to switch off the adjustment of outcomes to the distribution of outcomes and to model the change in education entirely as a result of the changing composition of parental education.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification EDUC_LEVEL4 //EN Education level
{
EL4_ISCED2, //EN ISCED 2-
EL4_ISCED3, //EN ISCED 3
EL4_ISCED4, //EN ISCED 4
EL4_ISCED5 //EN ISCED 5+
};
classification EDUC_LEVEL3 //EN Education level
{
EL3_LOW, //EN Low
EL3_MEDIUM, //EN Medium
EL3_HIGH //EN High
};
classification EDUC_TRANS //EN Education transitions
{
ETR_ISCED3, //EN ISCED2 -> ISCED3
ETR_ISCED4, //EN ISCED3 -> ISCED4
ETR_ISCED5 //EN ISCED4 -> ISCED5
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG_EDUCATION //EN Education
{
EducDistributionPara, EducOdds, FrozenEducCohort
};
parameters
{
double EducDistributionPara[SEX][EDUC_YOB][EDUC_LEVEL4]; //EN Education distribution
double EducOdds[SEX][PARENTS_EDUC3][EDUC_TRANS]; //EN Odds ratios education transitions
int FrozenEducCohort; //EN Last aligned education cohort
model_generated cumrate EducDistribution[SEX][EDUC_YOB][EDUC_LEVEL4]; //EN Education distribution
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
EDUC_LEVEL4 educ_level4 = { EL4_ISCED2 }; //EN Education level
EDUC_LEVEL4 educ_start = { EL4_ISCED2 }; //EN Education level in starting population
logical in_educ_start = { FALSE }; //EN In education in starting population
//EN Education level
EDUC_LEVEL3 educ_level3 = (educ_level4 == EL4_ISCED2) ? EL3_LOW :
(educ_level4 == EL4_ISCED5) ? EL3_HIGH : EL3_MEDIUM;
void setEducAtBirth(); //EN Set education at birth
EDUC_LEVEL4 getEducLevel(PARENTS_EDUC cParEduc); //EN Sample an education level
};
actor Observer
{
int educ_stack[EDUC_LEVEL4]; //EN Education stack
double frozen_educ_transition_rates[SEX][PARENTS_EDUC3][EDUC_TRANS]; //EN Education transition rates
logical educ_rates_frozen = { FALSE }; //EN Education transition rates are frozen
void resetEducStack(); //EN Reset education stack
void doAddEducToStack(EDUC_LEVEL4 cEduc); //EN Add to the education stack
bool getEducFromStack(EDUC_LEVEL4 cEduc); //EN Get education from stack
EDUC_LEVEL4 GetMostPopulatedEducFromStack(EDUC_LEVEL4 cEduc); //EN Return and decrement most populated possible education
bool hasThisOrHigherEducInStack(EDUC_LEVEL4 cEduc); //EN This or higher education in stack
double AdjustedProbability(double dProb, double dLogOdd, double dAdj); //EN Probability adjustment
event timeFreezeEducTransRatesEvent, FreezeEducTransRatesEvent; //EN Freeze education transition rates
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
bool Observer::getEducFromStack(EDUC_LEVEL4 cEduc)
{
bool bEducAvailable = FALSE;
if (educ_stack[cEduc] > 0)
{
educ_stack[cEduc] = educ_stack[cEduc] - 1;
bEducAvailable = TRUE;
}
return bEducAvailable;
}
bool Observer::hasThisOrHigherEducInStack(EDUC_LEVEL4 cEduc)
{
bool bEducAvailable = FALSE;
for (int nIndex = int(cEduc); nIndex < SIZE(EDUC_LEVEL4); nIndex++)
{
if (educ_stack[(EDUC_LEVEL4)nIndex] > 0) bEducAvailable = TRUE;
}
return bEducAvailable;
}
EDUC_LEVEL4 Observer::GetMostPopulatedEducFromStack(EDUC_LEVEL4 cEduc)
{
EDUC_LEVEL4 cReturnLevel = cEduc;
int nCount = 0;
for (int nIndex = int(cEduc); nIndex < SIZE(EDUC_LEVEL4); nIndex++)
{
if (educ_stack[(EDUC_LEVEL4)nIndex] > nCount)
{
nCount = educ_stack[(EDUC_LEVEL4)nIndex];
cReturnLevel = (EDUC_LEVEL4)nIndex;
}
}
educ_stack[cReturnLevel] = educ_stack[cReturnLevel] - 1;
return cReturnLevel;
}
void Observer::resetEducStack()
{
for (int nEduc = 0; nEduc < SIZE(EDUC_LEVEL4); nEduc++)
{
educ_stack[nEduc] = 0;
}
}
void Observer::doAddEducToStack(EDUC_LEVEL4 cEduc)
{
educ_stack[cEduc] = educ_stack[cEduc] + 1;
}
void Person::setEducAtBirth()
{
// Use info from starting population
if (creation_type == CT_START && year_of_birth < MIN(EDUC_YOB))
{
educ_level4 = educ_start;
}
// Cohorts which know parents education, (re)assign education (starting population info ignored)
else if ((creation_type == CT_START && year_of_birth > MAX(EDUC_IMPUTE)) || creation_type == CT_CHILD)
{
educ_level4 = getEducLevel(parents_educ);
}
// In-between cohorts from starting population, current school attendance or highest education reached to be respected
else if (creation_type == CT_START)
{
bool bIsSet = FALSE;
int nMaxIter = 100;
while (!bIsSet && nMaxIter > 0)
{
nMaxIter--;
// If not attending school or highest possibel level attained, startpop education is final fate
if (!in_educ_start || (int)educ_start == SIZE(EDUC_LEVEL4)-1)
{
if (lObserver->getEducFromStack(educ_start))
{
educ_level4 = educ_start;
bIsSet = TRUE;
}
else lObserver->doAddEducToStack(getEducLevel(PED_UNKNOWN));
}
// Education is at least as high as observed in starting population
else
{
if (lObserver->hasThisOrHigherEducInStack(educ_start))
{
educ_level4 = lObserver->GetMostPopulatedEducFromStack(educ_start);
bIsSet = TRUE;
}
else lObserver->doAddEducToStack(getEducLevel(PED_UNKNOWN));
}
}
if (!bIsSet) // this should happen only rarely
{
educ_level4 = getEducLevel(PED_UNKNOWN);
}
}
}
EDUC_LEVEL4 Person::getEducLevel(PARENTS_EDUC cParEduc)
{
EDUC_LEVEL4 cEducReturnValue = EL4_ISCED2;
int nEduc = 0;
// If parents education unknown just sample education
if (cParEduc == PED_UNKNOWN)
{
Lookup_EducDistribution(RandUniform(3), (int)sex, RANGE_POS(EDUC_YOB, (int)year_of_birth), &nEduc);
cEducReturnValue = (EDUC_LEVEL4)nEduc;
}
// If rates are frozen (no alignment to targets) use frozen rates
else if (lObserver->educ_rates_frozen)
{
bool bDoProgress = TRUE;
for (int nTransition = 0; nTransition < SIZE(EDUC_TRANS) && bDoProgress; nTransition++)
{
if (RandUniform(8) < lObserver->frozen_educ_transition_rates[sex][(PARENTS_EDUC3)int(cParEduc)][(EDUC_TRANS)nTransition]) nEduc++;
else bDoProgress = FALSE;
}
cEducReturnValue = (EDUC_LEVEL4)nEduc;
}
// find tranition rates which align to aggregate outcomes
else
{
///////////////////////////////
// First educational transition
// Distribution of parents education
double dParGroupShare[SIZE(PARENTS_EDUC3)];
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = lObserver->getShareParentsEduc((PARENTS_EDUC)nParGroup);
}
double dFactor1 = 1.0;
double dTargetProb = 1.0 - EducDistributionPara[sex][RANGE_POS(EDUC_YOB, year_of_birth)][EL4_ISCED2];
// Find probability based on odds and aligned to totals
if (dTargetProb == 1.0) cEducReturnValue = EL4_ISCED3;
else if (dTargetProb == 0.0) cEducReturnValue = EL4_ISCED2;
else
{
// Search for factor
int nIterations = 0;
double dResultProb = 10.0;
double dLower = -10.0;
double dUpper = 10.0;
double dCenter = 0.0;
while (abs(dResultProb - dTargetProb) > 0.0001 && nIterations < 10000)
{
nIterations++;
dCenter = (dLower + dUpper) / 2.0;
dResultProb = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dResultProb = dResultProb + dParGroupShare[nParGroup] *
lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][nParGroup][ETR_ISCED3]), dCenter);
}
if (dTargetProb > dResultProb) dLower = dCenter;
else dUpper = dCenter;
}
dFactor1 = dCenter;
// Check if individual transits to next level
double dIndividualProbability = lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][cParEduc][ETR_ISCED3]), dFactor1);
if (RandUniform(5) < dIndividualProbability) cEducReturnValue = EL4_ISCED3;
else cEducReturnValue = EL4_ISCED2;
}
// Continue to next transition?
if (cEducReturnValue == EL4_ISCED3)
{
///////////////////////////////
// Second educational transition
// Update distribution of parents education
double dSumShares = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] * lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][nParGroup][ETR_ISCED3]), dFactor1);
dSumShares = dSumShares + dParGroupShare[nParGroup];
}
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] / dSumShares;
}
// Find probability based on odds and aligned to totals
dTargetProb = (dTargetProb - EducDistributionPara[sex][RANGE_POS(EDUC_YOB, year_of_birth)][EL4_ISCED3]) / dTargetProb;
dFactor1 = 1.0;
if (dTargetProb == 1.0) cEducReturnValue = EL4_ISCED4;
else if (dTargetProb == 0.0) cEducReturnValue = EL4_ISCED3;
else
{
// Search for factor
int nIterations = 0;
double dResultProb = 10.0;
double dLower = -10.0;
double dUpper = 10.0;
double dCenter = 0.0;
while (abs(dResultProb - dTargetProb) > 0.0001 && nIterations < 10000)
{
nIterations++;
dCenter = (dLower + dUpper) / 2.0;
dResultProb = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dResultProb = dResultProb + dParGroupShare[nParGroup] *
lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][nParGroup][ETR_ISCED4]), dCenter);
}
if (dTargetProb > dResultProb) dLower = dCenter;
else dUpper = dCenter;
}
dFactor1 = dCenter;
// Check if individual transits to next level
double dIndividualProbability = lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][cParEduc][ETR_ISCED4]), dFactor1);
if (RandUniform(6) < dIndividualProbability) cEducReturnValue = EL4_ISCED4;
else cEducReturnValue = EL4_ISCED3;
}
// Continue to next transition?
if (cEducReturnValue == EL4_ISCED4)
{
///////////////////////////////
// Third educational transition
// Update distribution of parents education
double dSumShares = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] * lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][nParGroup][ETR_ISCED4]), dFactor1);
dSumShares = dSumShares + dParGroupShare[nParGroup];
}
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] / dSumShares;
}
// Find probability based on odds and aligned to totals
dTargetProb = EducDistributionPara[sex][RANGE_POS(EDUC_YOB, year_of_birth)][EL4_ISCED5] /
( EducDistributionPara[sex][RANGE_POS(EDUC_YOB, year_of_birth)][EL4_ISCED4]
+ EducDistributionPara[sex][RANGE_POS(EDUC_YOB, year_of_birth)][EL4_ISCED5]);
dFactor1 = 1.0;
if (dTargetProb == 1.0) cEducReturnValue = EL4_ISCED5;
else if (dTargetProb == 0.0) cEducReturnValue = EL4_ISCED4;
else
{
// Search for factor
int nIterations = 0;
double dResultProb = 10.0;
double dLower = -10.0;
double dUpper = 10.0;
double dCenter = 0.0;
while (abs(dResultProb - dTargetProb) > 0.0001 && nIterations < 10000)
{
nIterations++;
dCenter = (dLower + dUpper) / 2.0;
dResultProb = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dResultProb = dResultProb + dParGroupShare[nParGroup] *
lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][nParGroup][ETR_ISCED5]), dCenter);
}
if (dTargetProb > dResultProb) dLower = dCenter;
else dUpper = dCenter;
}
dFactor1 = dCenter;
// Check if individual transits to next level
double dIndividualProbability = lObserver->AdjustedProbability(dTargetProb, log(EducOdds[sex][cParEduc][ETR_ISCED5]), dFactor1);
if (RandUniform(7) < dIndividualProbability) cEducReturnValue = EL4_ISCED5;
else cEducReturnValue = EL4_ISCED4;
}
}
}
}
// Return education
return cEducReturnValue;
}
double Observer::AdjustedProbability(double dProb, double dLogOdd, double dAdj)
{
if (dProb <= 0.0) return 0.0;
else if (dProb >= 1.0) return 1.0;
else
{
if (dProb >= 0.9999) dProb = 0.9999;
double dValue = log(dProb / (1.0 - dProb)) + dLogOdd + dAdj;
if (dValue > 50) dValue = 50;
double dExp = exp(dValue);
return dExp / (1 + dExp);
}
}
TIME Observer::timeFreezeEducTransRatesEvent()
{
if (!educ_rates_frozen && FrozenEducCohort > MIN(EDUC_IMPUTE)) //TODO CHECK
{
return (double)FrozenEducCohort;
}
else return TIME_INFINITE;
}
void Observer::FreezeEducTransRatesEvent()
{
educ_rates_frozen = TRUE;
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
///////////////////////////////
// First educational transition
double dTargetProb = 1.0 - EducDistributionPara[nSex][RANGE_POS(EDUC_YOB, FrozenEducCohort)][EL4_ISCED2];
double dFactor1 = 1.0;
// Distribution of parents education
double dParGroupShare[SIZE(PARENTS_EDUC3)];
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = getShareParentsEduc((PARENTS_EDUC)nParGroup);
if (dTargetProb == 1.0) frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED3] = 1.0;
else if (dTargetProb == 0.0) frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED3] = 0.0;
}
// Find probability based on odds and aligned to totals
if (dTargetProb > 0.0 && dTargetProb < 1.0)
{
// Search for factor
int nIterations = 0;
double dResultProb = 10.0;
double dLower = -10.0;
double dUpper = 10.0;
double dCenter = 0.0;
while (abs(dResultProb - dTargetProb) > 0.0001 && nIterations < 10000)
{
nIterations++;
dCenter = (dLower + dUpper) / 2.0;
dResultProb = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dResultProb = dResultProb + dParGroupShare[nParGroup] *
AdjustedProbability(dTargetProb, log(EducOdds[nSex][nParGroup][ETR_ISCED3]), dCenter);
}
if (dTargetProb > dResultProb) dLower = dCenter;
else dUpper = dCenter;
}
dFactor1 = dCenter;
// Store transition rates
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED3] =
AdjustedProbability(dTargetProb, log(EducOdds[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED3]), dFactor1);
}
}
////////////////////////////////
// Second educational transition
if (dTargetProb > 0.0)
{
dTargetProb = (dTargetProb - EducDistributionPara[nSex][RANGE_POS(EDUC_YOB, FrozenEducCohort)][EL4_ISCED3]) / dTargetProb;
dFactor1 = 1.0;
// Update distribution of parents education
double dSumShares = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] * AdjustedProbability(dTargetProb, log(EducOdds[nSex][nParGroup][ETR_ISCED3]), dFactor1);
dSumShares = dSumShares + dParGroupShare[nParGroup];
}
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] / dSumShares;
if (dTargetProb == 1.0) frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED4] = 1.0;
else if (dTargetProb == 0.0) frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED4] = 0.0;
}
// Find probability based on odds and aligned to totals
if (dTargetProb > 0.0 && dTargetProb < 1.0)
{
// Search for factor
int nIterations = 0;
double dResultProb = 10.0;
double dLower = -10.0;
double dUpper = 10.0;
double dCenter = 0.0;
while (abs(dResultProb - dTargetProb) > 0.0001 && nIterations < 10000)
{
nIterations++;
dCenter = (dLower + dUpper) / 2.0;
dResultProb = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dResultProb = dResultProb + dParGroupShare[nParGroup] *
AdjustedProbability(dTargetProb, log(EducOdds[nSex][nParGroup][ETR_ISCED4]), dCenter);
}
if (dTargetProb > dResultProb) dLower = dCenter;
else dUpper = dCenter;
}
dFactor1 = dCenter;
// Store transition rates
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED4] =
AdjustedProbability(dTargetProb, log(EducOdds[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED4]), dFactor1);
}
}
}
///////////////////////////////
// Third educational transition
if (dTargetProb > 0.0)
{
dTargetProb = EducDistributionPara[nSex][RANGE_POS(EDUC_YOB, FrozenEducCohort)][EL4_ISCED5] /
(EducDistributionPara[nSex][RANGE_POS(EDUC_YOB, FrozenEducCohort)][EL4_ISCED4]
+ EducDistributionPara[nSex][RANGE_POS(EDUC_YOB, FrozenEducCohort)][EL4_ISCED5]);
dFactor1 = 1.0;
// Update distribution of parents education
double dSumShares = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] * AdjustedProbability(dTargetProb, log(EducOdds[nSex][nParGroup][ETR_ISCED4]), dFactor1);
dSumShares = dSumShares + dParGroupShare[nParGroup];
}
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dParGroupShare[nParGroup] = dParGroupShare[nParGroup] / dSumShares;
if (dTargetProb == 1.0) frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED5] = 1.0;
else if (dTargetProb == 0.0) frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED5] = 0.0;;
}
// Find probability based on odds and aligned to totals
if (dTargetProb > 0.0 && dTargetProb < 1.0)
{
// Search for factor
int nIterations = 0;
double dResultProb = 10.0;
double dLower = -10.0;
double dUpper = 10.0;
double dCenter = 0.0;
while (abs(dResultProb - dTargetProb) > 0.0001 && nIterations < 10000)
{
nIterations++;
dCenter = (dLower + dUpper) / 2.0;
dResultProb = 0.0;
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
dResultProb = dResultProb + dParGroupShare[nParGroup] *
AdjustedProbability(dTargetProb, log(EducOdds[nSex][nParGroup][ETR_ISCED5]), dCenter);
}
if (dTargetProb > dResultProb) dLower = dCenter;
else dUpper = dCenter;
}
dFactor1 = dCenter;
// Store transition rates
for (int nParGroup = 0; nParGroup < SIZE(PARENTS_EDUC3); nParGroup++)
{
frozen_educ_transition_rates[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED5] =
AdjustedProbability(dTargetProb, log(EducOdds[nSex][(PARENTS_EDUC3)nParGroup][ETR_ISCED5]), dFactor1);
}
}
}
}
}
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Presimulation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
void PreSimulation()
{
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
for (int nCohort = 0; nCohort < SIZE(EDUC_YOB); nCohort++)
{
for (int nEduc = 0; nEduc < SIZE(EDUC_LEVEL4); nEduc++)
{
EducDistribution[nSex][nCohort][nEduc] = EducDistributionPara[nSex][nCohort][nEduc];
}
}
}
}
Long-Term Care (LTC)
LongtermCare.mpp
This module implements long-term care needs, hours and care arrangements for people aged 65+ using a comparative approach described in detail in the technical paper Comparative Modelling of Long-Term Care in Hours. This novel approach generalises an Austrian administrative procedure for assessing care needs and uses data from the Survey of Health, Ageing and Retirement in Europe (SHARE) to quantify the demand for and supply of long-term care in hours, distinguishing between
Care provided in nursing homes
Formal home care
Informal care by spouses
Other informal care
Care gap
The model takes into account a wide range of factors that influence care needs and arrangements, including age, gender, education, the presence of a spouse able to provide care and the number of children. Compared to a macro approach based on age and gender, future care needs and demand, in particular for formal care and nursing homes, are mitigated by the expansion of education (better educated people tend to need less long-term care later in life), the modelling of partnerships (improvements in longevity increase the likelihood of living with a partner) and the consideration of mortality differences by education.
In the baseline scenario, needs and care arrangements are modelled based on individual and family characteristics “as of today”, with care provision adapting to current LTC patterns. The model includes scenario support that considers different dimensions of the drivers of future change.
Constrained supply scenarios: Users can set a growth path for the supply of care, including restrictions on the supply of nursing homes (compared to current places), restrictions on formal home care services (compared to current supply in hours), and restrictions on informal care provided by others other than spouses (typically children; the growth path is applied to the hours that would be available using current supply patterns).
Demographic scenarios, such as changes in mortality assumptions or partnership status.
Scenarios of changing care needs, such as “morbidity compression”, which assumes that improvements in longevity slow the age-related process of LTC needs. Such scenarios modify the individual age applied in the LTC models.
Scenarios involving compositional effects, such as the effect of educational expansion. This is realised by allowing education effects to be switched off (equivalent to applying current age-specific patterns) or by allowing convergence towards the patterns of the highest educated group. Education scenarios modify the individual education variable entering the LTC models.
The LTC module follows a cross-sectional imputation approach with monthly updates. The regression models are based on SHARE data with hours of care needs being imputed applying administrative procedures based on limitations in Activities of Daily Living (ADL) and limitations in Instrumental Activities of Daily Living (IADL) and other related variables available in the SHARE data. Within the simulation, each monthly update follows the following steps:
LTC Needs Assessment Step 1: Determine whether a person has care needs based on current prevalence by age, sex and education. Parameters are estimated using logistic regression.
LTC Needs Assessment Step 2: Determination of hours of care from distribution tables based on age, gender and education. Parameters estimated by quantile regression.
Nursing Homes: Probability of being in a nursing home based on current prevalence by age, intensity of need, availability of a spouse capable of providing care (not having own care needs above a threshold) and number of children. Parameters are estimated using logistic regression. If the scenario does not restrict/set the supply of nursing home care, these individual probabilities are used directly. If the supply is set by the user, the individual probabilities are converted into random waiting times that are used to rank people, and the ranking is then used to allocate available nursing home places.
LTC Mix Step 1: Probability of receiving (any) home care for people not living in a nursing home and not having a spouse able to provide care. If no care is received, the hours needed are recorded as a care gap. For persons with a spouse able to provide care, it is implicitly assumed that some care is received. This follows the logic of the SHARE survey, which does not quantify care gaps when a spouse is present.
LTC Mix Step 2: Determination of the provisional (“as of today”) home care mix if home care is received. Individuals are grouped according to the intensity of their care needs, the presence of a spouse capable of providing care, and the number of children. Within each group, the same (average) care mix is applied. The care mix distinguishes between formal care at home, informal care by a spouse, other informal care and a care gap.
LTC Mix Step 3: Determination of available care. With the exception of the calculation of the supply of care available from others when current patterns are applied (a parameter of average hours provided by age and gender), this step is scenario-based. It adds up the ‘provisional’ hours by type of home-care and compares them with the available supply of care for each type for which the given scenario sets/limits the supply. For each type of care, the proportion of demand met by supply is calculated. This step is skipped if there are no restrictions on the supply of care. If supply is restricted/fixed by the user, the provisional demand is adjusted and for each care type, the hours not met by the given supply are recorded. Similarly, oversupply is recorded. In the case of care gaps due to limited supply, it is determined whether there is a spouse who is potentially able to cover these hours. This information is recorded, but no assumptions are made about whether and how gaps are closed.
Key characteristics available for model output include hours of care needed and care mix, which distinguishes different types of potential care gaps:
Nursing homes: Hours provided; number of people in nursing homes
- Formal home care:
Hours met by current provision
Hours not covered by current supply (care gap due to supply constraints)
Hours exceeding current demand and available to fill gaps in care
- Hours of informal home-care provided by someone other than the spouse
Hours met by current supply patterns
Hours not covered by current supply patterns (care gap due to supply constraints)
Hours above current demand and available to fill care gaps
- Hours of informal home-care provided by spouse
Hours meeting current patterns
Potential additional hours to close gaps due to supply constraints in formal home care and informal care by others
- Care gap
Initial gap based on current patterns (people receiving no or insufficient care)
Additional gaps (or available additional supply) due to supply scenarios as listed above
Potential additional hours provided by spouses as listed above
Care hours by type of care are accumulated over the life course. Although the cross-sectional imputation approach does not allow a detailed longitudinal analysis of distributions, it is possible to compare average hours by care type for population groups distinguished by characteristics such as birth cohort, sex, number of children, partnership status at age 65 and education.
Model parameters:
Prevalence of having LTC needs (any hours) by sex, age, and education
Decile means of LTC hours needed by persons with care needs, by sex, age, and education
Nursing home prevalence by sex, partnership status, number of children, age group, and hours needed
Probability of receiving any home care among persons not in a nursing home and not having a partner able to provide care, by need in hours and number of children
Home care mix of persons not in a nursing home: mix as shares of hours by category, by partnership status, number of children, and LTC needs in hours
Average hours of informal care provided to persons aged 65 and over (excluding spouses), by age and sex
All parameters are estimated from SHARE data as described in detail in the technical report Comparative Modelling of Long-Term Care in Hours
Scenario parameters:
Slower ageing: parameters that allow the ageing process to be manipulated. Users can set a starting age from which the rate of ageing is changed; a second parameter sets the new length of each year. This allows individual ageing to be stretched, assuming that due to improvements in mortality, care needs and care hours increase more slowly with age. For example, the parameter can be set so that a person aged 65 will age 4 years in 5 years. A person aged 70 will then be 69, a person aged 75 will be 73… and 90 will be the new 85, thus adjusting age to increasing life expectancy.
Turn off the effects of educational composition: In this scenario, the composition of education by age and sex is held constant, which is equivalent to modelling care needs in hours without taking education into account. This scenario mimics a model that does not account for educational differences. Compared to other scenarios, it quantifies the compositional effect of educational improvements.
Matching LTC to supply: on/off switch by LTC type
LTC supply: future supply by LTC type and calendar year (current supply = 1.0)
Convergence of LTC needs with those of people with the highest level of education Convergence path by calendar year (0.0 - 1.0; 0.0 if no convergence). This provides an alternative to a ‘slower ageing’ scenario, assuming that the lower LTC needs of the better educated are determined by behaviours that can and will be adapted by others.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
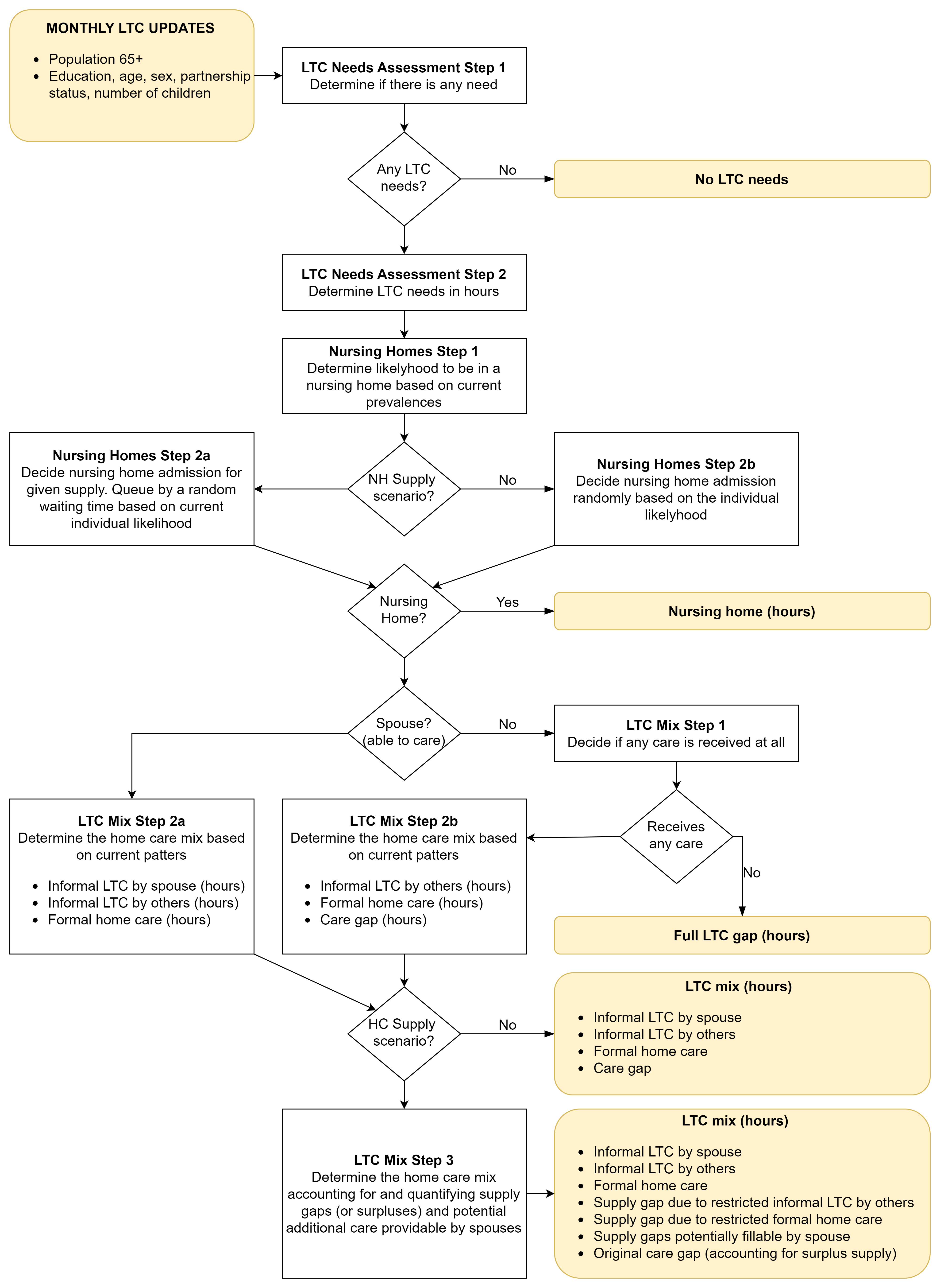
// Actor-Sets
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
//EN People waiting for place in nursing home
actor_set Person asPeopleWaitingForNursingHome
filter LtcAlignSupply[LAT_INST] && ltc_institution_wait < TIME_INFINITE && !in_care_home
order ltc_institution_wait;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Types
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
classification LTC_DECILE //EN Care deciles
{
CD_01, //EN Care decile 1
CD_02, //EN Care decile 2
CD_03, //EN Care decile 3
CD_04, //EN Care decile 4
CD_05, //EN Care decile 5
CD_06, //EN Care decile 6
CD_07, //EN Care decile 7
CD_08, //EN Care decile 8
CD_09, //EN Care decile 9
CD_10 //EN Care decile 10
};
classification SLOWER_AGEING_LTC //EN Slower Ageing Comparative LTC system
{
SAL_FROM_AGE, //EN From age
SAL_DURATION //EN Length of "slower" age year
};
classification ADULT_FAMILY_TYPE //EN Family type
{
AFT_SINGLE_0, //EN Single childless
AFT_SINGLE_1, //EN Single 1 child
AFT_SINGLE_2P, //EN Single 2+ children
AFT_COUPLE_0, //EN Couple childless
AFT_COUPLE_1, //EN Couple 1 child
AFT_COUPLE_2P //EN Couple 2+ children
};
classification CHILDREN //EN Children n/y
{
CHILD_NO, //EN Has no children
CHILD_YES //EN Has children
};
classification CHILDREN_GROUPED //EN Children grouped
{
CHILD_01, //EN Has 0-1 children
CHILD_2P //EN Has 2+ children
};
classification PARTNER //EN Partner
{
PARTNER_NO, //EN Has no partner
PARTNER_YES //EN Has partner
};
classification CARINGPARTNER //EN Caring partner
{
CPARTNER_NO, //EN Has no caring partner
CPARTNER_YES //EN Has caring partner
};
classification LTC_CARETYPE //EN Care type
{
LCA_FORMAL, //EN Formal Home Care
LCA_OTHER, //EN Informal other than partner
LCA_SPOUSE, //EN Partner
LCA_GAP //EN Gap
};
classification LTC_ALIGN_TYPES //EN Care types
{
LAT_INST, //EN Nursing homes
LAT_FORMAL, //EN Formal home care
LAT_OTHER //EN Informal other than partner
};
range AGE15P { 15, 105 }; //EN Age
range LTC_AGE { 65, 105 }; //EN Age
range LTC_NEEDHOURS { 0, 450 }; //EN LTC Hours
range LTC_COHORTS { 1953, 2072 }; //EN Birth cohort
partition LTC_COHORT //EN Birth cohort
{
1963, 1973, 1983, 1993, 2003, 2013, 2023, 2033, 2043, 2053, 2063
};
partition LTC_NEED { 20, 40, 120 }; //EN LTC Need
partition PART65PER5 { 70, 75, 80, 85, 90, 95 }; //EN Age group
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Parameters
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
parameter_group PG_LTC_COMPARATIVE //EN Comparative LTC system
{
PG_LTC_PARA,
PG_LTC_SCENARIOS
};
parameter_group PG_LTC_PARA //EN LTC Parameters
{
LtcAnyHours,
LtcHoursDecileMeans,
LtcNursingHome,
LtcAnyHomeCareReceivedNoPartner,
LtcHomeCareMix,
LtcCareGivingHours
};
parameter_group PG_LTC_SCENARIOS //EN LTC Scenario settings
{
LtcSlowerAgeingPara,
LtcAlignSupply,
LtcSupply,
LtcConvergenceEducation,
LtcSwitchEducationCompositionEffectsOff
};
parameters
{
// Model parameters
//EN Care prevalence any hours
double LtcAnyHours[SEX][LTC_AGE][EDUC_LEVEL3];
//EN Decile means of care hours
double LtcHoursDecileMeans[SEX][EDUC_LEVEL3][LTC_AGE][LTC_DECILE];
//EN Nursing home prevalence
double LtcNursingHome[SEX][PARTNER][NUMBER_CHILDREN2][LTC_AGE][LTC_NEED];
//EN Home care prevalence with need and no partner
double LtcAnyHomeCareReceivedNoPartner[LTC_NEEDHOURS][CHILDREN];
//EN Home care mix as a share of hours needed
double LtcHomeCareMix[CARINGPARTNER][CHILDREN_GROUPED][LTC_NEED][LTC_CARETYPE];
//EN Average hours of informal care given excl partner
double LtcCareGivingHours[AGE15P][SEX];
// Scenario parameters
double LtcSlowerAgeingPara[SLOWER_AGEING_LTC]; //EN Slower Ageing
logical LtcSwitchEducationCompositionEffectsOff; //EN Switch education composition effects off
logical LtcAlignSupply[LTC_ALIGN_TYPES]; //EN Align LTC to supply
double LtcSupply[LTC_ALIGN_TYPES][SIM_YEAR]; //EN LTC supply
double LtcConvergenceEducation[SIM_YEAR]; //EN LTC convergence to highest education (0 if non)
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Declarations
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
logical needs_ltc = { FALSE }; //EN Needs LT care
logical in_care_home = { FALSE }; //EN In care home
logical receives_any_home_care = { FALSE }; //EN Receives any home care
logical has_careable_partner = (has_spouse && !lSpouse->ltc_hours_180p);//EN Has a partner able to care
logical receives_care_from_partner = (ltc_hours_partner > 0.0); //EN Receives care from partner
double ltc_hours = { 0.0 }; //EN LT Care hours needed
double ltc_hours_institution = { 0.0 }; //EN Hours LTC in institution
double ltc_hours_formal = { 0.0 }; //EN Hours LTC formal home care
double ltc_hours_other = { 0.0 }; //EN Hours LTC informal home care others
double ltc_hours_partner = { 0.0 }; //EN Hours LTC informal home care partner
double ltc_hours_gap = { 0.0 }; //EN Hours LTC gap
double ltc_institution_prevalence = { 0.0 }; //EN Prevalence of institutionalisation
double ltc_institution_wait = { TIME_INFINITE }; //EN Waiting time institutionalisation
double ltc_hours_formal_excess = { 0.0 }; //EN Hours LTC formal home care excess supply
double ltc_hours_formal_gap = { 0.0 }; //EN Hours LTC formal home care not covered
double ltc_hours_other_excess = { 0.0 }; //EN Hours LTC informal home care excess supply
double ltc_hours_other_gap = { 0.0 }; //EN Hours LTC informal home care others not covered
double ltc_hours_partner_additional = { 0.0 }; //EN Hours LTC informal home care partner additional
//EN Hours LTC care by partner if supply gaps covered by partner
double ltc_hours_partner_total = ltc_hours_partner + ltc_hours_partner_additional;
double ltc_cumh_institution = 12.0 * weighted_duration(ltc_hours_institution); //EN Cumulated hours LTC in institution
double ltc_cumh_formal = 12.0 * weighted_duration(ltc_hours_formal); //EN Cumulated hours formal LTC
double ltc_cumh_other = 12.0 * weighted_duration(ltc_hours_other); //EN Cumulated hours informal LTC by others
double ltc_cumh_partner = 12.0 * weighted_duration(ltc_hours_partner); //EN Cumulated hours informal LTC by spouse
double ltc_cumh_gap = 12.0 * weighted_duration(ltc_hours_gap); //EN Cumulated hours LTC general gap
double ltc_cumh_formal_gap = 12.0 * weighted_duration(ltc_hours_formal_gap); //EN Cumulated hours LTC formal care supply gap
double ltc_cumh_other_gap = 12.0 * weighted_duration(ltc_hours_other_gap); //EN Cumulated hours LTC other care supply gap
double ltc_cum_lifetime = weighted_duration(ltc_in_longitudinal_sample); //EN Life expectancy 65+
double ltc_cum_partnertime = weighted_duration(ltc_in_longitudinal_sample, TRUE, has_spouse); //EN Time 65+ lived with a spouse
logical ltc_in_longitudinal_sample = { FALSE }; //EN Person in longitudinal LTC sample
logical ltc_longitudinal_has_partner = { FALSE }; //EN Person has partner at 65
//EN Family background
ADULT_FAMILY_TYPE adult_family_type =
(!has_spouse && number_children2 == NC2_0) ? AFT_SINGLE_0 :
(!has_spouse && number_children2 == NC2_1) ? AFT_SINGLE_1 :
(!has_spouse && number_children2 == NC2_2P) ? AFT_SINGLE_2P :
(has_spouse && number_children2 == NC2_0) ? AFT_COUPLE_0 :
(has_spouse && number_children2 == NC2_1) ? AFT_COUPLE_1 : AFT_COUPLE_2P;
logical ltc_hours_65p = (ltc_hours > 65.0); //EN LT Care more than 65 hours
logical ltc_hours_180p = (ltc_hours > 180.0); //EN LT Care more than 120 hours
int ltc_int_age = { 0 }; //EN Care age
LTC_AGE ltc_age = COERCE(LTC_AGE, ltc_int_age); //EN Care age
LTC_AGE ltc_real_age = COERCE(LTC_AGE, integer_age); //EN Care age
//EN Care provided to others than partner
double ltc_care_provided = (WITHIN(AGE15P, integer_age)) ?
LtcCareGivingHours[RANGE_POS(AGE15P,integer_age)][sex] : 0.0;
TIME time_next_ltc_age_update = { TIME_INFINITE }; //EN Time next ltv age update
event timeLtcAgeUpdateEvent, LtcAgeUpdateEvent; //EN LTC age update event
void InitTimeNextLtcAgeUpdate(); //EN Init next LTC age update
//hook InitTimeNextLtcAgeUpdate, SetAliveEvent, 5; //EN Hook init next care update
void doUpdateLtcNeeds(); //EN Update LTC needs
void doUpdateLtcPreliminaryMix(); //EN Update LTC mix - preliminary
void doUpdateLtcFinalMix(); //EN Update LTC mix - final
};
actor Observer
{
double ltc_initial_educ_composition[SEX][LTC_AGE][EDUC_LEVEL3]; //EN Initial education composition
// Initial LTC supply
double ltc_scaling_factor_others = { 1.0 }; //EN Scaling foctor others
double ltc_initial_supply_formal = { 0.0 }; //EN Initial LTC supply formal
double ltc_initial_supply_nursing = { 0.0 }; //EN Initial LTC supply nursing
double ltc_initial_supply_spouse = { 0.0 }; //EN Initial LTC supply spouse
double ltc_initial_supply_unmet = { 0.0 }; //EN Initial LTC care gap
logical ltc_initial_supply_is_set = { FALSE }; //EN Initial supply is set
// Current LTC demand & supply (patterns as of today)
double ltc_supply_others = { 0.0 }; //EN Current supply others
double ltc_demand_others = { 0.0 }; //EN Current demand others
double ltc_demand_formal = { 0.0 }; //EN Current demand formal
// Proportion LTC demand currently met
double ltc_propmet_other = { 0.0 }; //EN Proportion met demand informal others
double ltc_propmet_formal = { 0.0 }; //EN Proportion met demand formal
// Functions
void UpdateLontermCare(); //EN Update longterm care needs
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Implementation
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Maintain LTC age (ltc_int_age)
void Person::InitTimeNextLtcAgeUpdate()
{
ltc_int_age = 0;
if (time < MIN(SIM_YEAR) || integer_age < LtcSlowerAgeingPara[SAL_FROM_AGE]) time_next_ltc_age_update = WAIT(1.0);
else time_next_ltc_age_update = WAIT(LtcSlowerAgeingPara[SAL_DURATION]);
}
TIME Person::timeLtcAgeUpdateEvent() { return time_next_ltc_age_update; }
void Person::LtcAgeUpdateEvent()
{
// increment care age
if (ltc_int_age < MAX(LTC_AGE)) ltc_int_age++;
// set next event
if (time < MIN(SIM_YEAR) || integer_age < LtcSlowerAgeingPara[SAL_FROM_AGE]) time_next_ltc_age_update = WAIT(1.0);
else time_next_ltc_age_update = WAIT(LtcSlowerAgeingPara[SAL_DURATION]);
}
// Monthly update
void Observer::UpdateLontermCare()
{
/////////////////////////////////////////////////
// Initiate distributional table for education
/////////////////////////////////////////////////
if (!ltc_initial_supply_is_set && LtcSwitchEducationCompositionEffectsOff)
{
for (int nAge = MIN(LTC_AGE); nAge <= MAX(LTC_AGE); nAge++)
{
for (int nSex = 0; nSex < SIZE(SEX); nSex++)
{
double dPop = asResidentsAgeSex[nAge][nSex]->Count();
for (int nEduc = 0; nEduc < SIZE(EDUC_LEVEL3); nEduc++)
{
ltc_initial_educ_composition[nSex][RANGE_POS(LTC_AGE, nAge)][nEduc] = 0.0;
double nCell = asResidentsAgeSexEduc[nAge][nSex][nEduc]->Count();
if (dPop > 0.0) ltc_initial_educ_composition[nSex][RANGE_POS(LTC_AGE, nAge)][nEduc] = nCell / dPop;
}
}
}
}
/////////////////////////////////////////////////
// Care needs
/////////////////////////////////////////////////
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++) asAllPerson->Item(nJ)->doUpdateLtcNeeds();
/////////////////////////////////////////////////
// Institutionalisation
/////////////////////////////////////////////////
// if not aligned - or initial supply not set - use prevalences based on parameter
if (!LtcAlignSupply[LAT_INST] || !ltc_initial_supply_is_set)
{
ltc_initial_supply_nursing = 0.0;
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++)
{
Person_ptr ptrPerson = asAllPerson->Item(nJ);
if (RandUniform(56) < ptrPerson->ltc_institution_prevalence)
{
ptrPerson->in_care_home = TRUE;
ptrPerson->ltc_hours_institution = ptrPerson->ltc_hours;
ltc_initial_supply_nursing++;
}
}
}
// else fill available spaces
else
{
double dSupply = ltc_initial_supply_nursing * LtcSupply[LAT_INST][RANGE_POS(SIM_YEAR, observer_year)];
while (dSupply > 0.5 && asPeopleWaitingForNursingHome->Count() > 0)
{
Person_ptr ptrPerson = asPeopleWaitingForNursingHome->Item(0);
ptrPerson->in_care_home = TRUE;
ptrPerson->ltc_hours_institution = ptrPerson->ltc_hours;
dSupply--;
}
}
/////////////////////////////////////////////////
// Preliminary mix given institutionalisation
/////////////////////////////////////////////////
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++) asAllPerson->Item(nJ)->doUpdateLtcPreliminaryMix();
/////////////////////////////////////////////////
// Calculate available care
/////////////////////////////////////////////////
ltc_propmet_other = 1.0;
ltc_propmet_formal = 1.0;
// determine initial supply if not done yet
if (!ltc_initial_supply_is_set)
{
ltc_initial_supply_formal = 0.0;
ltc_scaling_factor_others = 1.0;
double dInitialDemandOthers = 0.0;
double dInitialSupplyOthers = 0.0;
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++)
{
Person_ptr ptrPerson = asAllPerson->Item(nJ);
dInitialSupplyOthers = dInitialSupplyOthers + ptrPerson->ltc_care_provided;
dInitialDemandOthers = dInitialDemandOthers + ptrPerson->ltc_hours_other;
ltc_initial_supply_formal = ltc_initial_supply_formal + ptrPerson->ltc_hours_formal;
}
ltc_scaling_factor_others = dInitialDemandOthers / dInitialSupplyOthers;
}
// calculate current demand and informal supply by others (as of today)
ltc_supply_others = 0.0;
ltc_demand_others = 0.0;
ltc_demand_formal = 0.0;
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++)
{
Person_ptr ptrPerson = asAllPerson->Item(nJ);
ltc_supply_others = ltc_supply_others + ptrPerson->ltc_care_provided;
ltc_demand_others = ltc_demand_others + ptrPerson->ltc_hours_other;
ltc_demand_formal = ltc_demand_formal + ptrPerson->ltc_hours_formal;
}
ltc_supply_others = ltc_supply_others * ltc_scaling_factor_others;
// Set avalable ptoportion of formal care and informal care by others
if (LtcAlignSupply[LAT_OTHER])
{
ltc_propmet_other = (ltc_supply_others * LtcSupply[LAT_OTHER][RANGE_POS(SIM_YEAR, observer_year)]) / ltc_demand_others;
}
if (LtcAlignSupply[LAT_FORMAL])
{
ltc_propmet_formal = (ltc_initial_supply_formal * LtcSupply[LAT_FORMAL][RANGE_POS(SIM_YEAR, observer_year)]) / ltc_demand_formal;
}
// update LTC final mix (accounting fo supply) for all
for (long nJ = 0; nJ < asAllPerson->Count(); nJ++) asAllPerson->Item(nJ)->doUpdateLtcFinalMix();
ltc_initial_supply_is_set = TRUE;
}
// Individual care needs
void Person::doUpdateLtcNeeds()
{
// reset
needs_ltc = FALSE;
ltc_hours = 0.0;
ltc_hours_institution = 0.0;
ltc_hours_formal = 0.0;
ltc_hours_other = 0.0;
ltc_hours_partner = 0.0;
ltc_hours_gap = 0.0;
ltc_institution_prevalence = 0.0;
ltc_institution_wait = TIME_INFINITE;
in_care_home = FALSE;
ltc_hours_formal_excess = 0.0;
ltc_hours_formal_gap = 0.0;
ltc_hours_other_excess = 0.0;
ltc_hours_other_gap = 0.0;
ltc_hours_partner_additional = 0.0 ;
// update need for care
if ( WITHIN(LTC_AGE, ltc_int_age) && is_resident )
{
EDUC_LEVEL3 cCareEduc = educ_level3;
// re-sample education in case of "no composition effects" scenario
if (LtcSwitchEducationCompositionEffectsOff)
{
double dRandom = RandUniform(59);
if (dRandom < lObserver->ltc_initial_educ_composition[sex][RANGE_POS(LTC_AGE, integer_age)][EL3_LOW]) cCareEduc = EL3_LOW;
else if (dRandom < lObserver->ltc_initial_educ_composition[sex][RANGE_POS(LTC_AGE, integer_age)][EL3_LOW]
+ lObserver->ltc_initial_educ_composition[sex][RANGE_POS(LTC_AGE, integer_age)][EL3_MEDIUM]) cCareEduc = EL3_MEDIUM;
else cCareEduc = EL3_HIGH;
}
// modify education in case of convergence scenario
if (RandUniform(57) < LtcConvergenceEducation[RANGE_POS(SIM_YEAR, calendar_year)]) cCareEduc = EL3_HIGH;
// decide if any care needed
if (RandUniform(82) < LtcAnyHours[sex][RANGE_POS(LTC_AGE, ltc_age)][cCareEduc]) needs_ltc = TRUE;
else needs_ltc = FALSE;
// decide hours of care needed
if (needs_ltc)
{
int nDecile = int(RandUniform(83) * 10.0);
ltc_hours = LtcHoursDecileMeans[sex][cCareEduc][RANGE_POS(LTC_AGE, ltc_age)][nDecile];
if (ltc_hours < 0.0) ltc_hours = 0.0;
}
else ltc_hours = 0.0;
// prevalence of institutionalisation as in parameter and derived waiting time for ranking
ltc_institution_prevalence = LtcNursingHome[sex][(PARTNER)(int)has_spouse][number_children2][RANGE_POS(LTC_AGE, ltc_age)][SPLIT(ltc_hours, LTC_NEED)];
if (ltc_institution_prevalence > 0.99) ltc_institution_prevalence = 0.99;
if (ltc_institution_prevalence > 0.0)
{
ltc_institution_wait = log(RandUniform(54)) / log(1.0 - ltc_institution_prevalence);
}
else ltc_institution_wait = TIME_INFINITE;
}
}
// Individual care mix after institutionalisation is decided - preliminary
void Person::doUpdateLtcPreliminaryMix()
{
if (needs_ltc && !in_care_home)
{
// has a partner able to care
if (has_careable_partner) receives_any_home_care = TRUE;
// has no such partner
else
{
CHILDREN cChildren = CHILD_NO;
if (number_children2 != NC2_0) cChildren = CHILD_YES;
double dProbReceiveCare = LtcAnyHomeCareReceivedNoPartner[(LTC_NEEDHOURS)COERCE(LTC_NEEDHOURS, ltc_hours)][cChildren];
if (RandUniform(55) < dProbReceiveCare) receives_any_home_care = TRUE;
else
{
receives_any_home_care = FALSE;
ltc_hours_gap = ltc_hours;
}
}
}
else receives_any_home_care = FALSE;
// home care mix
if (receives_any_home_care)
{
CHILDREN_GROUPED cChildrenGrouped = CHILD_01;
if (number_children2 == NC2_2P) cChildrenGrouped = CHILD_2P;
CARINGPARTNER cCaringPartner = (CARINGPARTNER)(int)has_careable_partner;
ltc_hours_formal = ltc_hours * LtcHomeCareMix[cCaringPartner][cChildrenGrouped][SPLIT(ltc_hours, LTC_NEED)][LCA_FORMAL]; // Formal Home Care
ltc_hours_other = ltc_hours * LtcHomeCareMix[cCaringPartner][cChildrenGrouped][SPLIT(ltc_hours, LTC_NEED)][LCA_OTHER]; // Informal other than partner
ltc_hours_partner = ltc_hours * LtcHomeCareMix[cCaringPartner][cChildrenGrouped][SPLIT(ltc_hours, LTC_NEED)][LCA_SPOUSE]; // Partner
ltc_hours_gap = ltc_hours * LtcHomeCareMix[cCaringPartner][cChildrenGrouped][SPLIT(ltc_hours, LTC_NEED)][LCA_GAP]; // Gap
}
}
// Individual care mix after institutionalisation is decided - final
void Person::doUpdateLtcFinalMix()
{
// final home care mix
if (receives_any_home_care)
{
if (lObserver->ltc_propmet_formal > 1) ltc_hours_formal_excess = (lObserver->ltc_propmet_formal - 1) * ltc_hours_formal;
else if (lObserver->ltc_propmet_formal < 1)
{
ltc_hours_formal_gap = (1 - lObserver->ltc_propmet_formal) * ltc_hours_formal;
ltc_hours_formal = lObserver->ltc_propmet_formal * ltc_hours_formal;
}
if (lObserver->ltc_propmet_other > 1) ltc_hours_other_excess = (lObserver->ltc_propmet_other - 1) * ltc_hours_other;
else if (lObserver->ltc_propmet_other < 1)
{
ltc_hours_other_gap = (1 - lObserver->ltc_propmet_other) * ltc_hours_other;
ltc_hours_other = lObserver->ltc_propmet_other * ltc_hours_other;
}
if (has_careable_partner) ltc_hours_partner_additional = ltc_hours_other_gap + ltc_hours_formal_gap;
}
}
Model Output
TablesDemography.mpp
Demographic tables include tables of the projected population by age, sex and education, tables of demographic events such as births and deaths, and detailed tables on fertility and migration.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table states
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
SIM_TO_2050 yob_sim_to_2050 = COERCE(SIM_TO_2050, year_of_birth); //EN Year of birth
//EN Year of birth
YOB_1930_TO_2050 yob_1930_to_2050 = COERCE(YOB_1930_TO_2050, year_of_birth);
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table groups
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table_group TG_DEMOGRAPHY //EN General demography
{
tabCohortLifeExpectancy,
tabTotalPopulation,
tabDemographicEvents
};
table_group TG_MIGRATION //EN Migration
{
tabMigrationByAgeSex,
tabUnattendedImmigrants
};
table_group TG_FERTILITY //EN Fertility
{
tabBirthPeriodMeasures,
tabAverageAgeAtBirth,
tabCompletedFertility
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Tables
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// General demography
table Person tabCohortLifeExpectancy //EN Cohort life expectancy
[creation_type == CT_CHILD && is_resident && WITHIN(SIM_TO_2050,year_of_birth)]
{
sex+ *
{
//EN Life expectancy decimals=2
value_at_transitions(is_alive,TRUE,FALSE,age) / transitions(is_alive,TRUE,FALSE)
}
* yob_sim_to_2050 //EN Year of birth
* educ_level3+ //EN Education
};
table Person tabTotalPopulation //EN Total Population
[in_projected_time && is_resident]
{
sex+ * //EN Sex
{
duration() //EN Population decimals=0
}
* integer_age + //EN Age
* sim_year //EN Year
};
table Person tabDemographicEvents //EN Demographic events
[in_projected_time && (is_resident || (!is_resident && is_alive))]
{
sex+ *
sim_year * //EN Year
{
entrances(is_alive,TRUE), //EN Births decimals=0
entrances(is_alive,FALSE), //EN Deaths decimals=0
entrances(is_resident, TRUE), //EN Immigrants decimals=0
entrances(is_resident, FALSE) //EN Emigrants decimals=0
} //EN Demographic events
};
// Migration
table Person tabMigrationByAgeSex //EN Migration by age and sex
[in_projected_time]
{
sex + * //EN Sex
{
entrances(is_resident,TRUE), //EN Immigrants decimals=0
entrances(is_resident,FALSE), //EN Emigrants decimals=0
entrances(is_resident,TRUE) - entrances(is_resident,FALSE) //EN Net migration
} //EN Displayed measure
* integer_age + //EN Age
* sim_year //EN Year
};
table Person tabUnattendedImmigrants //EN Share unattended immigrants
[in_projected_time && creation_type == CT_IMMIGRANT]
{
{
//EN Share entering unattended decimals=3
value_at_transitions(is_resident,FALSE,TRUE,is_unattended) / transitions(is_resident,FALSE,TRUE),
//EN Share resident immigrants being unattended decimals=3
weighted_duration(is_resident,TRUE,is_unattended) / duration(is_resident,TRUE)
} //EN Displayed measure
* integer_age //EN Age
* sim_year //EN Year
};
// Fertility
table Person tabBirthPeriodMeasures //EN Birth period measures
[sex == FEMALE && is_resident && in_projected_time && WITHIN(FERTILE_AGE,integer_age)]
{
educ_level3+ * //EN Education
{
//EN Birth rate decimals=3
sim_births / duration(),
//EN First birth rate decimals=3
entrances(number_children2,NC2_1) / duration(),
//EN Second birth rate decimals=3
entrances(number_children2,NC2_2P) / duration(),
//EN Third and higher birth rate decimals=3
sim_higher_births / duration(),
//EN First birth hazard decimals=3
entrances(number_children2,NC2_1) / duration(number_children2,NC2_0),
//EN Second birth hazard decimals=3
entrances(number_children2,NC2_2P) / duration(number_children2,NC2_1),
//EN Third and higher birth hazard decimals=3
sim_higher_births / duration(number_children2,NC2_2P),
//EN Births decimals=0
sim_births,
//EN First births decimals=0
entrances(number_children2,NC2_1),
//EN Second births decimals=0
entrances(number_children2,NC2_2P),
//EN Third and higher births decimals=0
sim_higher_births
} //EN Displayed measure
* fertile_age //EN Age
* sim_year //EN Year
};
table Person tabAverageAgeAtBirth //EN Average age at birth
[sex == FEMALE && is_resident && in_projected_time ]
{
{
//EN Average age at birth decimals=2
value_at_changes(sim_births,age) / changes(sim_births),
//EN Average age at first birth decimals=2
value_at_entrances(number_children2, NC2_1 ,age) / entrances(number_children2, NC2_1)
} //EN Displayed measure
* sim_year //EN Year
* educ_level3+ //EN Education
};
table Person tabCompletedFertility //EN Completed fertility
[ is_resident && trigger_entrances(is_alive, FALSE) && WITHIN(YOB_1930_TO_2050, year_of_birth)]
{
sex+ * //EN Sex
educ_level3 + * //EN Education
{
unit //EN Persons decimals=0
}
* yob_1930_to_2050 //EN Year of birth
* number_children2 //EN Children
};
TablesEducation.mpp
Education tables present simulation outputs concerning both own and parents’ education.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table groups
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table_group TG_EDUCATION //EN Education
{
tabEducationYob,
tabEducationYobParents
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Tables
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table Person tabEducationYob //EN Education by year of birth
[integer_age == 0]
{
parents_educ+ * //EN Parents education
sex+ * //EN Sex
{
duration(educ_level4,EL4_ISCED2) / duration(), //EN ISCED 2 decimals=3
duration(educ_level4,EL4_ISCED3) / duration(), //EN ISCED 3 decimals=3
duration(educ_level4,EL4_ISCED4) / duration(), //EN ISCED 4 decimals=3
duration(educ_level4,EL4_ISCED5) / duration(), //EN ISCED 5+ decimals=3
duration(parents_educ,PED_UNKNOWN) / duration() //EN Parents education unknown decimals=3
} //EN Education characteristics
* year_of_birth //EN Year of birth
};
table Person tabEducationYobParents //EN Parents education by year of birth
[trigger_entrances(is_alive, TRUE)]
{
creation_type + * //EN [V] Creation type
{
unit //EN Persons decimals=0
} //EN Persons by education of parents
* calendar_year //EN Year of birth
* parents_educ //EN Parents education
};
TablesFamily.mpp
Families tables provide output concerning family sizes and other family characteristics.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table dimensions
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
partition TIME_PERIOD { 2025, 2035, 2045, 2055, 2065 }; //EN Time period
partition AGE_P10 { 15, 25, 35, 45, 55, 65, 75, 85 }; //EN Age group
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table states
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
//EN In partnership childless
logical has_spouse_childless = (has_spouse && number_children2 == NC2_0);
//EN In partnership one child
logical has_spouse_child_1 = (has_spouse && number_children2 == NC2_1);
//EN In partnership two+ children
logical has_spouse_child_2p = (has_spouse && number_children2 == NC2_2P);
//EN No partnership childless
logical no_spouse_childless = (!has_spouse && number_children2 == NC2_0);
//EN No partnership one child
logical no_spouse_child_1 = (!has_spouse && number_children2 == NC2_1);
//EN No partnership two+ children
logical no_spouse_child_2p = (!has_spouse && number_children2 == NC2_2P);
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table groups
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table_group TG_FAMILY //EN Family
{
tabLivingWithParents,
tabFamilySizeAtStart,
tabFamily65p,
tabFamilyAgeGrYear
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Tables
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table Person tabLivingWithParents //EN Living with parents
[in_projected_time && is_resident && WITHIN(AGE_MAX26, integer_age)]
{
sex + * //EN Sex
split(calendar_year, TIME_PERIOD) + * //EN Time period
age_max26 * //EN Age
{
duration(lives_with_father,TRUE) / duration(), //EN Living with father decimals=3
duration(lives_with_mother,TRUE) / duration(), //EN Living with mother decimals=3
duration(lives_with_parents,TRUE) / duration(), //EN Living with any parent decimals=3
duration(lives_with_two_parents,TRUE) / duration() //EN Living with two parents decimals=3
} //EN Proportions
};
table Person tabFamilySizeAtStart //EN Family compositions at start
[trigger_entrances(in_projected_time, TRUE) && is_resident]
{
sex + * //EN Sex
has_spouse + * //EN Has spouse
{
unit //EN Persons decimals=0
}
* integer_age //EN Age
* number_children2 + //EN Number of children
};
table Person tabFamily65p //EN Family background 65+
[in_projected_time && is_resident && WITHIN(AGE_65P, integer_age) ]
{
sex+ * //EN Sex
educ_level3+ * //EN Education
//EN Time period
split(calendar_year, TIME_PERIOD) *
//EN Age
age_65p *
{
duration(has_spouse_childless, TRUE) / duration(), //EN In partnership childless decimals=3
duration(has_spouse_child_1, TRUE) / duration(), //EN In partnership one child decimals=3
duration(has_spouse_child_2p, TRUE) / duration(), //EN In partnership two+ children decimals=3
duration(no_spouse_childless, TRUE) / duration(), //EN No partnership childless decimals=3
duration(no_spouse_child_1, TRUE) / duration(), //EN No partnership one child decimals=3
duration(no_spouse_child_2p, TRUE) / duration() //EN No partnership two+ children decimals=3
} //EN Proportions
};
table Person tabFamilyAgeGrYear //EN Family background age group year
[in_projected_time && is_resident]
{
sex + * //EN Sex
educ_level3 + * //EN Education
split(integer_age, AGE_P10)+ * //EN Age group
{
duration(has_spouse, TRUE) / duration(), //EN In partnership decimals=3
duration(has_spouse_childless, TRUE) / duration(), //EN In partnership childless decimals=3
duration(has_spouse_child_1, TRUE) / duration(), //EN In partnership one child decimals=3
duration(has_spouse_child_2p, TRUE) / duration(), //EN In partnership two+ children decimals=3
duration(no_spouse_childless, TRUE) / duration(), //EN No partnership childless decimals=3
duration(no_spouse_child_1, TRUE) / duration(), //EN No partnership one child decimals=3
duration(no_spouse_child_2p, TRUE) / duration() //EN No partnership two+ children decimals=3
} //EN Proportions
* sim_year
};
TablesLongtermCare.mpp
The LTC tables provide a rich output on LTC needs in hours and the mix of care received by those in need of care. Results are presented from both a period and a longitudinal perspective, the latter accumulating LTC hours by type of care over the life course by birth cohort, sex and education.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Dimensions
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
partition TAB_CARE_HOURS { 30, 60, 90, 120, 150, 180, 210 }; //EN Care hours
partition TAB_DECADES { 2028, 2038, 2048, 2058, 2068, 2078 }; //EN Years
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table groups
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table_group TG_LTC //EN Long-Term Care
{
tabLtCareAge,
tabLtCareHours,
tabLtCareHoursMix,
tabLtCareProvided,
tabCareFromPartner,
tabCohortCare
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Tables
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table Person tabLtCareAge //EN [LTC_COMP] Average LTC care age by age
[year_of_birth == MIN(SIM_YEAR)]
{
integer_age* //EN Age
{
weighted_duration(ltc_int_age) / duration() //EN LTC age decimals=3
}
};
table Person tabLtCareHours //EN [LTC_COMP] LTC care
[in_projected_time && WITHIN(LTC_AGE, integer_age) && is_resident]
{
sex + * //EN Sex
educ_level3 + * //EN Education
{
weighted_duration(needs_ltc) / duration(), //EN Proportion any LTC needs decimals=2
weighted_duration(ltc_hours_65p) / duration(), //EN Proportion LTC 65+ hours decimals=2
weighted_duration(ltc_hours) / duration(), //EN Average LTC hours all decimals=2
weighted_duration(ltc_hours) / weighted_duration(needs_ltc), //EN Average LTC hours of receivers decimals=2
duration(needs_ltc,TRUE), //EN Number receivers
weighted_duration(ltc_hours) //EN Total needed hours
}
* split(ltc_real_age, PART65PER5) + //EN Age
* sim_year //EN Year
};
table Person tabLtCareHoursMix //EN [LTC_COMP] LTC care mix
[in_projected_time && WITHIN(LTC_AGE, integer_age) && needs_ltc && is_resident]
{
{
//EN Proportion hours in institutions decimals=2
weighted_duration(ltc_hours_institution) / weighted_duration(ltc_hours),
//EN Proportion hours formal home decimals=2
weighted_duration(ltc_hours_formal) / weighted_duration(ltc_hours),
//EN Proportion hours informal home care others decimals=2
weighted_duration(ltc_hours_other) / weighted_duration(ltc_hours),
//EN Proportion hours informal home care partner decimals=2
weighted_duration(ltc_hours_partner) / weighted_duration(ltc_hours),
//EN Proportion hours gap decimals=2
weighted_duration(ltc_hours_gap) / weighted_duration(ltc_hours) ,
//EN Proportion hours unmet formal home decimals=2
weighted_duration(ltc_hours_formal_gap) / weighted_duration(ltc_hours),
//EN Proportion hours excess formal home decimals=2
weighted_duration(ltc_hours_formal_excess) / weighted_duration(ltc_hours),
//EN Proportion hours unmet other home decimals=2
weighted_duration(ltc_hours_other_gap) / weighted_duration(ltc_hours),
//EN Proportion hours excess other home decimals=2
weighted_duration(ltc_hours_other_excess) / weighted_duration(ltc_hours),
weighted_duration(ltc_hours) / duration(), //EN Average needed hours decimals=2
weighted_duration(ltc_hours_institution) , //EN hours in institutions
weighted_duration(ltc_hours_formal) , //EN hours formal home
weighted_duration(ltc_hours_other) , //EN hours informal home other
weighted_duration(ltc_hours_partner) , //EN hours informal home partner
weighted_duration(ltc_hours_gap), //EN hours gap
weighted_duration(ltc_hours), //EN Total hours
weighted_duration(ltc_hours_formal_gap), //EN hours formal unmet (supply gap)
weighted_duration(ltc_hours_formal_excess), //EN hours formal excess (additional supply)
weighted_duration(ltc_hours_other_gap), //EN hours other unmet (supply gap)
weighted_duration(ltc_hours_other_excess), //EN hours excess other (additional ssupply)
weighted_duration(ltc_hours_partner_additional) //EN hours supply gap potentially coverable by partner
} //EN Care mix measures
* sim_year //EN Hours
};
table Person tabLtCareProvided //EN [LTC_COMP] LTC care provided to others than partner
[in_projected_time && is_resident]
{
{
weighted_duration(ltc_care_provided) //EN Total hours of care provided
}
* sim_year //EN Year
* sex + //EN Sex
};
table Person tabCareFromPartner //EN [LTC_COMP] Total care from partner if covering supply gaps
[receives_care_from_partner && in_projected_time && is_resident]
{
sex+ * //EN Sex of care receiver
{
duration() //EN Persons
}
* split(ltc_hours_partner_total,TAB_CARE_HOURS) + //EN Duration
* split(sim_year,TAB_DECADES) //EN Decade
};
table Person tabCohortCare //EN [LTC_COMP] Average care hours over lifecourse
[ltc_in_longitudinal_sample && trigger_entrances(is_alive, FALSE) && is_resident]
{
sex + * //EN Sex
educ_level3 + * //EN Education
{
unit, //EN Persons
value_in(ltc_cumh_institution) / unit, //EN Cumulated hours LTC in institution
value_in(ltc_cumh_formal) / unit, //EN Cumulated hours formal LTC
value_in(ltc_cumh_other) / unit, //EN Cumulated hours informal LTC by others
value_in(ltc_cumh_partner) / unit, //EN Cumulated hours informal LTC by spouse
value_in(ltc_cumh_gap) / unit, //EN Cumulated hours LTC general gap
value_in(ltc_cumh_formal_gap) / unit, //EN Cumulated hours LTC formal care supply gap
value_in(ltc_cumh_other_gap) / unit, //EN Cumulated hours LTC others care supply gap
value_in(ltc_cum_lifetime) / unit //EN Life expectancy 65+
} //EN Cumulative measures
* split(year_of_birth, LTC_COHORT) //EN Birth cohort
};
TablesValidation.mpp
Validation tables present simulation results that can be directly compared to model parameters.
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table states
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
actor Person
{
YOB_BIRTH1 yob_birth1 = COERCE(YOB_BIRTH1, year_of_birth); //EN Year of birth
FERT_PROG fert_prog = COERCE(FERT_PROG,years_since_first_birth); //EN Years since first birth
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Table groups
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table_group TG_VALIDATION //EN Validation
{
tabPartnershipStatusMothers,
tabPartnershipStatusChildless,
tabPartnershipAge,
tabFirstBirthRates,
tabSecondBirthRates
};
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// Tables
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
table Person tabFirstBirthRates //EN [V] First birth rates
[sex == FEMALE && in_projected_time && is_resident && number_children2 == NC2_0 && WITHIN(YOB_BIRTH1, year_of_birth)]
{
educ_level3 + * //EN Education
{
entrances(number_children2,NC2_1) / duration() //EN First birth rate decimals=3
}
* fertile_age //EN Age
* yob_birth1 //EN Year of birth
};
table Person tabSecondBirthRates //EN [V] Second birth rates
[sex == FEMALE && in_projected_time && is_resident
&& number_children2 == NC2_1 && WITHIN(YOB_BIRTH1, year_of_birth)
&& WITHIN(FERT_PROG, years_since_first_birth)]
{
educ_level3 + * //EN Education
{
entrances(number_children2,NC2_2P) / duration() //EN Second birth rate decimals=3
}
* fert_prog
* yob_birth1 //EN Year of birth
};
table Person tabPartnershipStatusMothers //EN [V] Partnership Status Mothers
[in_projected_time && sex == FEMALE && children_in_family > 0 && is_resident]
{
educ_level3 + * //EN Education
{
duration(has_spouse,TRUE) / duration() //EN Has spouse decimals=3
}
* moth_agegr //EN Age group mother
* child_agegr //EN Child age group
};
table Person tabPartnershipStatusChildless //EN [V] Partnership Status Childless
[in_projected_time && sex==FEMALE && children_in_family==0 && is_resident && WITHIN(SPOUSE_AGE, integer_age)]
{
{
duration(has_spouse,TRUE) / duration() //EN Has spouse decimals=3
}
* partnership_age //EN Age
* educ_level3 + //EN Education
};
table Person tabPartnershipAge //EN [V] Partner age distribution after 2050
[sim_year > 2050 && sex == FEMALE && has_spouse && is_resident && WITHIN(SPOUSE_AGE, integer_age)]
{
{
duration() //EN Persons decimals=0
}
* partnership_age //EN Age
* partnership_spouse_age //EN Spouse age
};